题目内容
7.数列{an}满足a2=2,an+2+(-1)n+1an=1+(-1)n(n∈N*),S n为数列{an}前n项和,S100=( )| A. | 5100 | B. | 2550 | C. | 2500 | D. | 2450 |
分析 数列{an}满足a2=2,an+2+(-1)n+1an=1+(-1)n(n∈N*),n=2k(k∈N*)时,a2k+2-a2k=2,因此数列{a2k}为等差数列,首项为2,公差为2.n=2k-1(k∈N*)时,a2k+1+a2k-1=0.通过分组求和,利用等差数列的求和公式即可得出.
解答 解:数列{an}满足a2=2,an+2+(-1)n+1an=1+(-1)n(n∈N*),
n=2k(k∈N*)时,a2k+2-a2k=2,因此数列{a2k}为等差数列,首项为2,公差为2.
n=2k-1(k∈N*)时,a2k+1+a2k-1=0.
∴S100=(a1+a3+…+a97+a99)+(a2+a4+…+a100)
=0+2×50+$\frac{50×49}{2}×2$=2550.
故选:B.
点评 本题考查了等差数列的通项公式与求和公式、数列递推关系、分类讨论方法、分组求和,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
16.已知i为虚数单位,复数z满足i•z=(1-2i)2,则|z|的值为( )
| A. | 2 | B. | 3 | C. | $2\sqrt{3}$ | D. | 5 |
17.已知某几何体的三视图如图所示,则该几何体的体积为( )
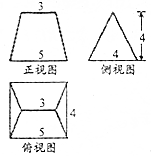

| A. | $\frac{113}{3}$ | B. | 35 | C. | $\frac{104}{3}$ | D. | $\frac{107}{4}$ |
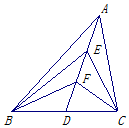 如图,在△ABC中,D为BC的中点,E,F为AD上的两个三等分点.若$\overrightarrow{BE}•\overrightarrow{CE}=\frac{7}{8}$,$BC=\frac{{\sqrt{26}}}{2}$,则$\overrightarrow{BF}•\overrightarrow{CF}$=-$\frac{17}{8}$.
如图,在△ABC中,D为BC的中点,E,F为AD上的两个三等分点.若$\overrightarrow{BE}•\overrightarrow{CE}=\frac{7}{8}$,$BC=\frac{{\sqrt{26}}}{2}$,则$\overrightarrow{BF}•\overrightarrow{CF}$=-$\frac{17}{8}$.