题目内容
5.设实数a∈(0,1),则函数f(x)=x2-(2a+1)x+a2+1有零点的概率为( )| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
分析 由二次函数所对应二次方程的判别式大于等于0求得a的范围,结合a∈(0,1)可得a所在区间长度,利用区间长度比可得函数f(x)=x2-(2a+1)x+a2+1有零点的概率.
解答 解:若函数f(x)=x2-(2a+1)x+a2+1有零点,
则△=[-(2a+1)]2-4(a2+1)=4a2+4a+1-4a2-4=4a-3≥0,
即a$≥\frac{3}{4}$.
又∵a∈(0,1),
∴a∈($\frac{3}{4},1$),
∴函数f(x)=x2-(2a+1)x+a2+1有零点的概率为$\frac{1-\frac{3}{4}}{1-0}=\frac{1}{4}$.
故选:D.
点评 本题考查几何概型,考查了二次函数零点的判定方法,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.已知数列{an}满足a1=1,${a_2}=\frac{1}{3}$,若${a_n}({a_{n-1}}+2{a_{n+1}})=3{a_{n-1}}•{a_{n+1}}(n≥2,n∈{N^*})$,则数列{an}的通项an=( )
| A. | $\frac{1}{{{2^{n-1}}}}$ | B. | $\frac{1}{{{2^n}-1}}$ | C. | $\frac{1}{{{3^{n-1}}}}$ | D. | $\frac{1}{{{2^{n-1}}+1}}$ |
16.已知i为虚数单位,复数z满足i•z=(1-2i)2,则|z|的值为( )
| A. | 2 | B. | 3 | C. | $2\sqrt{3}$ | D. | 5 |
13.有三名男生和3名女生参加演讲比赛,每人依次按顺序出场比赛,若出场时相邻两个女生之间至少间隔一名男生,则共有( )种不同的排法.
| A. | 108 | B. | 120 | C. | 72 | D. | 144 |
17.已知某几何体的三视图如图所示,则该几何体的体积为( )
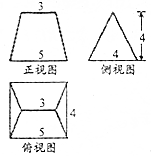

| A. | $\frac{113}{3}$ | B. | 35 | C. | $\frac{104}{3}$ | D. | $\frac{107}{4}$ |