题目内容

6．在等差数列{an}中，已知a4=5，a3是a2和a6的等比中项，则数列{an}的前5项的和为（　　）
A．15B．20C．25D．15或25

分析 利用等差数列的通项公式和等比中项定义，列出方程组，求出a1=-1，d=2，由此能求出数列{an}的前5项的和．

解答 解：∵在等差数列{an}中，a4=5，
a3是a2和a6的等比中项，
∴$\left\{\begin{array}{l}{{a}_{1}+3d=5}\\{（{a}_{1}+2d）^{2}=（{a}_{1}+d）（{a}_{1}+5d）}\end{array}\right.$，
解得a1=-1，d=2，
∴数列{an}的前5项的和为：
${S}_{5}=5{a}_{1}+\frac{5×4}{2}d$=5×（-1）+5×4=15．
故选：A．

点评 本题考查等差数列的前五项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．

练习册系列答案
相关题目
16．已知n=3${∫}_{1}^{e}$$\frac{1}{x}$dx，在（x+2$\sqrt{x}$+1）n的展开式中，x2的系数是15（用数字填写答案）
17．已知u，v是方程x2-4tx-1=0（t∈R）的两个不相等的实数根，函数f（x）=$\frac{x-2t}{2{x}^{2}+2}$的定义域为[u，v]，它的最大值、最小值分别记为f（x）max，f（x）min
（I）当t=0时，求f（x）max，f（x）min
（II）令g（t）=f（x）max-f（x）min，求函数g（t）的解析式．
14．如图1，菱形ABCD的边长为12，∠BAD=60°，AC与BD交于O点．将菱形ABCD沿对角线AC折起，得到三棱锥B-ACD，点M是棱BC的中点，DM=6$\sqrt{2}$．

（ I）求证：平面ODM⊥平面ABC；
（ II）求二面角M-AD-C的余弦值．
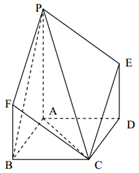1．如图，点P是菱形ABCD所在平面外一点，PA⊥平面ABCD，PA∥FB∥ED，∠ABC=60°，PA=AB=2BF=2DE．
（Ⅰ）求证：平面PAC⊥平面PCE；
（Ⅱ）求二面角B-PC-F的余弦值．
11．下列命题中，正确的命题序号是①③④．
①已知a∈R，两直线l1：ax+y=1，l2：x+ay=2a，则“a=-1”是“l1∥l2”的充分条件；
②命题p：“?x≥0，2x＞x2”的否定是“?x0≥0，2x0＜x02”；
③“sinα=$\frac{1}{2}$”是“α=2kπ+$\frac{π}{6}$，k∈Z”的必要条件；
④已知a＞0，b＞0，则“ab＞1”的充要条件是“a＞$\frac{1}{b}$”．
18．如图是八位同学400米测试成绩的茎叶图（单位：秒），则（　　）
A．平均数为64B．众数为7C．极差为17D．中位数为64.5
15．已知数列{an}满足a1=1，${a_2}=\frac{1}{3}$，若${a_n}（{a_{n-1}}+2{a_{n+1}}）=3{a_{n-1}}•{a_{n+1}}（n≥2，n∈{N^*}）$，则数列{an}的通项an=（　　）
A．$\frac{1}{{{2^{n-1}}}}$B．$\frac{1}{{{2^n}-1}}$C．$\frac{1}{{{3^{n-1}}}}$D．$\frac{1}{{{2^{n-1}}+1}}$
16．已知i为虚数单位，复数z满足i•z=（1-2i）2，则|z|的值为（　　）
A．2B．3C．$2\sqrt{3}$D．5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网