��Ŀ����
��֪���κ���f��x��=ax2+x������?x��[0��1]��f��x����1����������ʵ��a��ȡֵ��Χ��
f��x����1?ax2+x��1��x��[0��1]����
��x=0ʱ��a��0����ʽ��Ȼ������
��x�ʣ�0��1]ʱ����ʽ��Ϊa��
-
��x�ʣ�0��1]�Ϻ������
��t=
����t��[1��+�ޣ�������a��t2-t������ֻ��a�ܣ�t2-t��min=0
⇒a��0����a��0����a��0
���ϣ�����ʵ��a��ȡֵ��Χ�� ��
f��x����1?ax2+x��1��x��[0��1]����
��x=0ʱ��a��0����ʽ��Ȼ������
��x�ʣ�0��1]ʱ����ʽ��Ϊa��
| 1 |
| x2 |
| 1 |
| x |
��t=
| 1 |
| x |
⇒a��0����a��0����a��0
���ϣ�����ʵ��a��ȡֵ��Χ��
���㣺���κ���������
ר�⣺���������ʼ�Ӧ��
���������������Ǻ��������ʽ��ͨ���α������룬�õ�a��
-
������º���g��x��=
-
��x�ʣ�0��1]����Сֵ���õ�������ۣ�
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
���
�⣺��f��x����1��
��ax2+x��1��x��[0��1]����
��1����x=0ʱ��a��0����ʽ��Ȼ������
��2����x�ʣ�0��1]ʱ����ʽ��Ϊa��
-
��x�ʣ�0��1]�Ϻ������
��t=
����t��[1��+�ޣ�������a��t2-t��
����ֻ��a�ܣ�t2-t��min=0
��a��0��
�֡�a��0��
��a��0��
�ʴ�Ϊ����-�ޣ�0����
��ax2+x��1��x��[0��1]����
��1����x=0ʱ��a��0����ʽ��Ȼ������
��2����x�ʣ�0��1]ʱ����ʽ��Ϊa��
| 1 |
| x2 |
| 1 |
| x |
��t=
| 1 |
| x |
����ֻ��a�ܣ�t2-t��min=0
��a��0��
�֡�a��0��
��a��0��
�ʴ�Ϊ����-�ޣ�0����
���������⿼����Ǻ�������⣬�����˲α������룬�����ѶȲ������ڻ����⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
����{an}������Ϊ1��{bn}����2Ϊ�����2Ϊ���ȵĵȱ����У���bn=an+1-an��n��N*����an=��������
| A��2n-1 |
| B��2n |
| C��2n+1-1 |
| D��2n-2 |
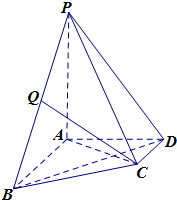 ��ͼ��������P-ABCD�У�AB��CD��AB��AD��AB=4��AD=2
��ͼ��������P-ABCD�У�AB��CD��AB��AD��AB=4��AD=2