题目内容
已知函数f（x）=asin（πx+a）+bcos（πx+β）+1，且f（2006）=-1，求f（2007）的值．
考点：对数函数的单调性与特殊点
专题：函数的性质及应用
分析：由条件利用诱导公式求得asina+bsinb的值，再利用诱导公式求得f（2007）的值．
解答：
解：由题意可得f（2006）=asin（2006π+a）+bcos（2006π+β）+1=asina+bsinb+1=-1，
∴asina+bsinb=-2．
故f（2007）=asin（2007π+a）+bcos（2007π+b）+1=-asina-bcosb+1=2+1=3．
∴asina+bsinb=-2．
故f（2007）=asin（2007π+a）+bcos（2007π+b）+1=-asina-bcosb+1=2+1=3．
点评：本题主要考查诱导公式的应用，求出asina+bsinb的值，是解题的关键，属于基础题．
练习册系列答案
相关题目
函数y=esinx（-π≤x≤π）的大致图象为（ ）
A、 |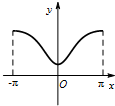
B、 |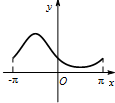
C、 |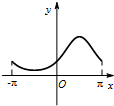
D、 |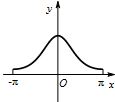
程序框图如图，若输出的s值为两位数时，则n的值为（ ）| A、3 | B、4 | C、5 | D、6 |
在正方体ABCD-A1B1C1D1中，若E是B1D1的中点，则直线BE垂直于（ ）
| A、AC |
| B、BD |
| C、A1D |
| D、A1D1 |