题目内容
10. 如图,三棱柱ABC-A1B1C1的各条棱长都是$\sqrt{2}$,且顶点A1在底面ABC上的射影O为△ABC的中心,则三棱锥A1-ABC的体积为$\frac{1}{3}$.
如图,三棱柱ABC-A1B1C1的各条棱长都是$\sqrt{2}$,且顶点A1在底面ABC上的射影O为△ABC的中心,则三棱锥A1-ABC的体积为$\frac{1}{3}$.
分析 由题意可知,O为底面正三角形的重心,由重心的性质求得OA,进一步求出三棱锥的高,代入体积公式得答案.
解答 解:如图,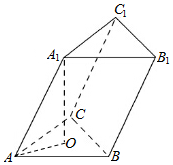
由题意可知,底面三角形ABC为正三角形,
由O为△ABC的中心,可知O为△ABC的外心,
则O为底面高的$\frac{2}{3}$,
∵底面三角形的边长为$\sqrt{2}$,
∴底面三角形的高为$\sqrt{(\sqrt{2})^{2}-(\frac{\sqrt{2}}{2})^{2}}=\frac{\sqrt{6}}{2}$,
∴OA=$\frac{\sqrt{6}}{3}$,
在Rt△A1AO中,由${A}_{1}A=\sqrt{2},OA=\frac{\sqrt{6}}{3}$,得$O{A}_{1}=\sqrt{(\sqrt{2})^{2}-(\frac{\sqrt{6}}{3})^{2}}=\frac{2\sqrt{3}}{3}$,
∴三棱锥A1-ABC的体积为$\frac{1}{3}×\frac{1}{2}×\sqrt{2}×\frac{\sqrt{6}}{2}×\frac{2\sqrt{3}}{3}=\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查锥体体积的求法,关键是掌握三角形重心的性质,是中档题.

练习册系列答案
相关题目
2.设集合A={x|$\frac{2016-x}{x-2015}$≥0},B={x|y=lg2(x-2015)<1},则A∪B( )
| A. | {x|2015<x≤2016} | B. | {x|2015<x<2016} | C. | (2015,2017) | D. | {x|x<2017} |
19.已知向量$\overrightarrow{OA}$,$\overrightarrow{OB}$垂直,且|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=24,若t∈[0,1],则|t$\overrightarrow{AB}$-$\overrightarrow{AO}$|+|$\frac{5}{12}$$\overrightarrow{BO}$-(1-t)$\overrightarrow{BA}$|的最小值为( )
| A. | 2$\sqrt{193}$ | B. | 26 | C. | 17$\sqrt{2}$ | D. | 24 |
20.下列直线与圆(x-1)2+(y+2)2=5相切的是( )
| A. | 2x-y+1=0 | B. | 2x-y-1=0 | C. | 2x+y+1=0 | D. | 2x+y-1=0 |
 某苗圃基地为了解基地内甲、乙两块地种植的同一种树苗的长势情况,从两块地各随机抽取了10株树苗,分别测出它们的高度如下(单位:cm)
某苗圃基地为了解基地内甲、乙两块地种植的同一种树苗的长势情况,从两块地各随机抽取了10株树苗,分别测出它们的高度如下(单位:cm)