题目内容
函数f(x)=C
x4+C
x3+C
x2+C
x+C
图象的对称轴方程为 .
0 4 |
1 4 |
2 4 |
3 4 |
4 4 |
考点:二项式定理的应用,二项式系数的性质
专题:计算题,函数的性质及应用,二项式定理
分析:利用二项式定理化简函数的表达式,然后求解函数的对称轴方程.
解答:
解:由函数f(x)=C
x4+C
x3+C
x2+C
x+C
=(1+x)4,
∴函数的对称轴方程为x=-1.
故答案为:x=-1.
0 4 |
1 4 |
2 4 |
3 4 |
4 4 |
=(1+x)4,
∴函数的对称轴方程为x=-1.
故答案为:x=-1.
点评:本题考查二项式定理的应用,函数的对称轴的求法,基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合A={x|y=
},B={x|
≤0},则A∩B=( )
| x+1 |
| x-1 |
| x+1 |
| A、(-1,1] |
| B、[-1,1] |
| C、[1,+∞) |
| D、[0,1] |
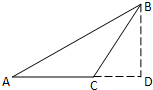 已知△ABC为等腰三角形,∠A=∠B=30°,BD为AC边上的高,若
已知△ABC为等腰三角形,∠A=∠B=30°,BD为AC边上的高,若| AB |
| a |
| AC |
| b |
| BD |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
设a,b,c∈R,且a<b,则( )
| A、ac>bc | ||||
B、
| ||||
| C、a2>b2 | ||||
| D、a3<b3 |
已知直线l的斜率为k(k≠0),它在x轴、y轴上的截距分别为k、2k,则直线l的方程为( )
| A、2x-y-4=0 |
| B、2x-y+4=0 |
| C、2x+y-4=0 |
| D、2x+y+4=0 |