题目内容
12.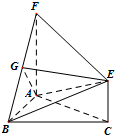 如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF$\stackrel{∥}{=}$2CE,G是线段BF上一点,AB=AF=BC.
如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF$\stackrel{∥}{=}$2CE,G是线段BF上一点,AB=AF=BC.(Ⅰ)若EG∥平面ABC,求$\frac{BG}{BF}$的值;
(Ⅱ)求二面角A-BF-E的大小的正弦值.
分析 (Ⅰ)由平面ABC⊥平面ACEF,且平面ABC∩平面ACEF=AC,可得AF⊥AC,则AF⊥平面ABC,得到平面ABF⊥平面ABC,过G作GD⊥AB,垂足为D,则GD⊥平面ABC,连接CD,可证得则四边形GDCF为平行四边形,从而得到GD=CE=$\frac{1}{2}AF$,则G为BF的中点,得到$\frac{BG}{BF}$的值;
(Ⅱ)建立空间直角坐标系,利用向量法即可求二面角E-BF-A的余弦值.
解答 解:(Ⅰ)∵平面ABC⊥平面ACEF,且平面ABC∩平面ACEF=AC,
AF⊥AC,∴AF⊥平面ABC,则平面ABF⊥平面ABC,
过G作GD⊥AB,垂足为D,则GD⊥平面ABC,连接CD,
由GD⊥平面ABC,AF⊥平面ABC,AF∥CE,可得GD∥CE,
又EG∥平面ABC,∴EG∥CD,则四边形GDCF为平行四边形,
∴GD=CE=$\frac{1}{2}AF$,
∴$\frac{BG}{BF}$=$\frac{1}{2}$;
(Ⅱ)由(Ⅰ)知AF⊥AB,AF⊥BC
∵BC⊥AB,∴BC⊥平面ABF.
如图,以A为原点,建立空间直角坐标系A-xyz.
则F(0,0,2),B(2,0,0),C(2,2,0),E(2,2,1),
$\overrightarrow{BC}$=(0,2,0)是平面ABF的一个法向量.
设平面BEF的法向量$\overrightarrow{n}$=(x,y,z),则
$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BE}=2y+z=0}\\{\overrightarrow{n}•\overrightarrow{BF}=-2x+2z=0}\end{array}\right.$,令y=1,则z=-2,x=-2,$\overrightarrow{n}$=(-2,1,-2),
∴cos<$\overrightarrow{n}$,$\overrightarrow{BC}$>=$\frac{\overrightarrow{n}•\overrightarrow{BC}}{|\overrightarrow{n}||\overrightarrow{BC}|}$=$\frac{1}{3}$,
∴二面角A-BF-E的正弦值为$\sqrt{1-(\frac{1}{3})^{2}}=\frac{2\sqrt{2}}{3}$.
点评 本题主要考查线面平行的判定以及空间二面角的计算,建立空间直角坐标系,利用向量法是解决本题的关键,是中档题.

| A. | 命题“?x0∈R,x02-x0≤0”的否定为“?x∈R,x2-x>0” | |
| B. | 命题“在△ABC中,A>30°,则sinA>$\frac{1}{2}$”的逆否命题为真命题 | |
| C. | 设{an}是公比为q的等比数列,则“q>1”是“{an}为递增数列”的充分必要条件 | |
| D. | 若非零向量$\overrightarrow a$、$\overrightarrow b$满足$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|+|{\overrightarrow b}$|,则$\overrightarrow a$与$\overrightarrow b$共线 |
| A. | -2 | B. | -2017 | C. | 2017 | D. | 2 |
| A. | $-\frac{11}{13}$ | B. | $-\frac{11}{12}$ | C. | $-\frac{7}{12}$ | D. | $-\frac{1}{13}$ |
| A. | [0,+∞) | B. | (0,+∞) | C. | (1,2) | D. | (1,+∞) |
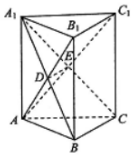 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,A1B与AB1交于点D,A1C与AC1交于点E.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,A1B与AB1交于点D,A1C与AC1交于点E.