题目内容
20.已知函数f(x)的定义域为R,当x<0时,f(x)=x3-1;当-1≤x≤1时,f(-x)=f(x);当x>$\frac{1}{2}$时,f(x+$\frac{1}{2}$)=f(x-$\frac{1}{2}$).则f(2017)=( )| A. | -2 | B. | -2017 | C. | 2017 | D. | 2 |
分析 当x>$\frac{1}{2}$时,函数f(x)是周期为1的周期函数,由题意昨f(2017)=f(1)=-f(-1),由此能求出结果.
解答 解:∵当x>$\frac{1}{2}$时,f(x+$\frac{1}{2}$)=f(x-$\frac{1}{2}$),
∴当x>$\frac{1}{2}$时,函数f(x)是周期为1的周期函数,
∵函数f(x)的定义域为R,当x<0时,f(x)=x3-1;当-1≤x≤1时,f(-x)=f(x)
∴f(2017)=f(1)=-f(-1)=-[(-1)3-1]=2.
故选:D.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的离心率为( )
| A. | $\frac{5}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
5.设集合A={x|x2-3x<0},B={x||x|>2},则A∩B=( )
| A. | (2,3) | B. | (-2,3) | C. | (0,2) | D. | (-2,0) |
9.下列函数中哪个与函数y=-x相等( )
| A. | $y=-\sqrt{x^2}$ | B. | $y=\frac{-x(x-1)}{x-1}$ | ||
| C. | y=-logaax(a>0且a≠1) | D. | $y=-\sqrt{x}•\sqrt{x}$ |
13.某程序框图如图所示,该程序运行后输出的S的值是( )


| A. | 2015 | B. | 2016 | C. | 3024 | D. | 1007 |
 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b分别为9,15,则输出的a=( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b分别为9,15,则输出的a=( )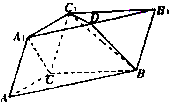 在三棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=120°,D为A1B1的中点.
在三棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=120°,D为A1B1的中点.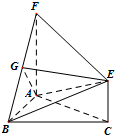 如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF$\stackrel{∥}{=}$2CE,G是线段BF上一点,AB=AF=BC.
如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF$\stackrel{∥}{=}$2CE,G是线段BF上一点,AB=AF=BC.