题目内容
2.下列选项中,说法正确的是( )| A. | 命题“?x0∈R,x02-x0≤0”的否定为“?x∈R,x2-x>0” | |
| B. | 命题“在△ABC中,A>30°,则sinA>$\frac{1}{2}$”的逆否命题为真命题 | |
| C. | 设{an}是公比为q的等比数列,则“q>1”是“{an}为递增数列”的充分必要条件 | |
| D. | 若非零向量$\overrightarrow a$、$\overrightarrow b$满足$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|+|{\overrightarrow b}$|,则$\overrightarrow a$与$\overrightarrow b$共线 |
分析 由特称命题的否定为全称命题,即可判断A;由A=150°,可得sinA=$\frac{1}{2}$,再结合原命题与逆否命题等价,即可判断B;由a1<0,0<q<1,即可判断C;再由向量共线的条件,即可判断D.
解答 解:对于A,由特称命题的否定为全称命题,可得命题“?x0∈R,x02-x0≤0”
的否定为“?x∈R,x2-x>0”,故A错;
对于B,命题“在△ABC中,A>30°,则sinA>$\frac{1}{2}$”为假命题,比如A=150°,则sinA=$\frac{1}{2}$.
再由原命题与其逆否命题等价,则其逆否命题为假命题,故B错;
对于C,设{an}是公比为q的等比数列,则“q>1”推不出“{an}为递增数列”,比如a1<0,不为增函数;
反之,可得0<q<1.故不为充分必要条件,故C错;
对于D,若非零向量$\overrightarrow a$、$\overrightarrow b$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$|,则$\overrightarrow{a}$,$\overrightarrow{b}$同向,则$\overrightarrow a$与$\overrightarrow b$共线,故D正确.
故选:D.
点评 本题考查命题的真假判断,主要是命题的否定、四种命题的真假、充分必要条件的判断和向量共线的条件,考查判断和推理能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.设M、N是直线x+y-2=0上的两动点,且|MN|=$\sqrt{2}$,则$\overrightarrow{OM}$•$\overrightarrow{ON}$的最小值为( )
| A. | 1 | B. | 2 | C. | $\frac{5}{2}$ | D. | $\frac{3}{2}$ |
 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b分别为9,15,则输出的a=( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b分别为9,15,则输出的a=( )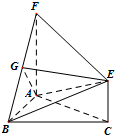 如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF$\stackrel{∥}{=}$2CE,G是线段BF上一点,AB=AF=BC.
如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF$\stackrel{∥}{=}$2CE,G是线段BF上一点,AB=AF=BC.