题目内容
4.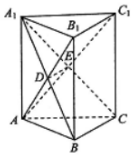 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,A1B与AB1交于点D,A1C与AC1交于点E.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,A1B与AB1交于点D,A1C与AC1交于点E.求证:(1)DE∥平面B1BCC1;
(2)平面A1BC⊥平面A1ACC1.
分析 (1)利用三角形中位线的性质证明DE∥BC,即可证明DE∥平面B1BCC1;
(2)证明BC⊥平面A1ACC1,即可证明平面A1BC⊥平面A1ACC1.
解答 证明:(1)由题意,D,E分别为A1B,A1C的中点,
∴DE∥BC,
∵DE?平面B1BCC1,BC?平面B1BCC1,
∴DE∥平面B1BCC1;
(2)∵AA1⊥平面ABC,BC?平面ABC,
∴AA1⊥BC,
∵AC⊥BC,AC∩AA1=A,
∴BC⊥平面A1ACC1,
∵BC?平面A1BC,
∴平面A1BC⊥平面A1ACC1.
点评 本题主要考查了直线与平面平行的判定,直线与平面垂直的判定,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的离心率为( )
| A. | $\frac{5}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
9.下列函数中哪个与函数y=-x相等( )
| A. | $y=-\sqrt{x^2}$ | B. | $y=\frac{-x(x-1)}{x-1}$ | ||
| C. | y=-logaax(a>0且a≠1) | D. | $y=-\sqrt{x}•\sqrt{x}$ |
17.在数列{an}中,已知a1=3,且数列{an+(-1)n}是公比为2的等比数列,对于任意的n∈N*,不等式a1+a2+…+an≥λan+1恒成立,则实数λ的取值范围是( )
| A. | $({-∞,\frac{2}{5}}]$ | B. | $({-∞,\frac{1}{2}}]$ | C. | $({-∞,\frac{2}{3}}]$ | D. | (-∞,1] |
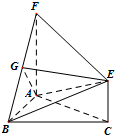 如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF$\stackrel{∥}{=}$2CE,G是线段BF上一点,AB=AF=BC.
如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF$\stackrel{∥}{=}$2CE,G是线段BF上一点,AB=AF=BC.