题目内容
3.命题“?x∈N,x2>1”的否定为?x0∈N,x02≤1.分析 直接利用全称命题的否定是特称命题,写出结果即可.
解答 解:因为全称命题的否定是特称命题,所以,命题“?x∈N,x2>1”的否定为?x0∈N,x02≤1
故答案为:?x0∈N,x02≤1
点评 本题考查命题的否定,全称命题与特称命题的否定关系,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.若双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的中心在坐标原点O,过C的右顶点和右焦点分别作垂直于x轴的直线,交C的渐近线于A,B和M,N,若△OAB与△OMN的面积之比为1:4,则C的渐近线方程为( )
| A. | y=±x | B. | $y=±\sqrt{3}x$ | C. | y=±2x | D. | y=±3x |
15.双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的离心率为( )
| A. | $\frac{5}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b分别为9,15,则输出的a=( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b分别为9,15,则输出的a=( )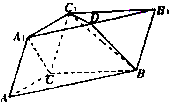 在三棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=120°,D为A1B1的中点.
在三棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=120°,D为A1B1的中点.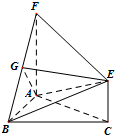 如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF$\stackrel{∥}{=}$2CE,G是线段BF上一点,AB=AF=BC.
如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF$\stackrel{∥}{=}$2CE,G是线段BF上一点,AB=AF=BC.