题目内容
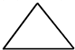
若一个正四棱锥的左视图是一个边长为2的正三角形（如图），则该正四棱锥的体积是（ ）
| A、1 | ||||
B、
| ||||
C、
| ||||
D、2
|
考点：棱柱、棱锥、棱台的体积
专题：空间位置关系与距离
分析：三视图复原的几何体是正四棱锥，求出底面面积，正四棱锥的高，即可求出体积．
解答：
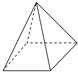解：如图据条件可得几何体为底面边长为2的正方形，侧面是等腰三角形，
斜高为2，棱锥的高为
的正四棱锥，
故其体积V=
×4×
=
．
故选：C．
解：如图据条件可得几何体为底面边长为2的正方形，侧面是等腰三角形，斜高为2，棱锥的高为
| 22-1 |
故其体积V=
| 1 |
| 3 |
| 22-1 |
4
| ||
| 3 |
故选：C．
点评：本题是基础题，考查几何体的三视图，几何体的体积的求法，准确判断几何体的形状是解题的关键．
练习册系列答案
导学全程练创优训练系列答案
相关题目
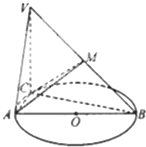如图，已知⊙O的直径AB=3，点C为⊙O上异于A、B的一点，VC⊥平面ABC，且VC=2，点M为线段VB的中点．（Ⅰ）求证：BC⊥平面VAC在平行四边形ABCD中，
=3
，AE的延长线与CD交于点F，若
=
，
=
，则
=（ ）
| BD |
| ED |
| AC |
| a |
| BD |
| b |
| AF |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
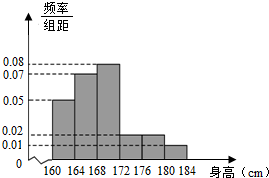贵州省2014年全省高中男生身高统计调查数据显示：全省100000名男生的身高服从正态分布N（168，16）．现从某学校高三年级男生中随机抽取50名测量身高，测量发现被测学生身高全部介于160cm和184cm之间，将测量结果按如下方式分成6组：第1组[160，164），第2组[164，168），…，第6组[180，184]，如图是按上述分组方法得到的频率分布直方图．设函数f（x）=|lnx|-
的两个零点为x1，x2，则有（ ）
| 1 |
| x+1 |
| A、x1x2＜1 | ||
| B、x1x2=1 | ||
C、1＜x1x2＜
| ||
D、x1x2≥
|