题目内容
在平行四边形ABCD中,
=3
,AE的延长线与CD交于点F,若
=
,
=
,则
=( )
| BD |
| ED |
| AC |
| a |
| BD |
| b |
| AF |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:如图所示,由
=3
,可得
=2
,因此
=2
,即点F是CD的中点.由
+
=
,
-
=
,可得
=
(
+
)=
(
+
).
利用
=
+
即可得出.
| BD |
| ED |
| BE |
| ED |
| AB |
| DF |
| AD |
| AB |
| AC |
| AD |
| AB |
| BD |
| AD |
| 1 |
| 2 |
| AC |
| BD |
| 1 |
| 2 |
| a |
| b |
利用
| AF |
| 1 |
| 2 |
| AC |
| 1 |
| 2 |
| AD |
解答:
解:如图所示,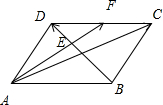
∵
=3
,
∴
=2
,
∴
=2
,即点F是CD的中点.
∵
+
=
,
-
=
,
∴
=
(
+
)=
(
+
).
∴
=
+
=
+
×
(
+
)
=
+
.
故选:B.

∵
| BD |
| ED |
∴
| BE |
| ED |
∴
| AB |
| DF |
∵
| AD |
| AB |
| AC |
| AD |
| AB |
| BD |
∴
| AD |
| 1 |
| 2 |
| AC |
| BD |
| 1 |
| 2 |
| a |
| b |
∴
| AF |
| 1 |
| 2 |
| AC |
| 1 |
| 2 |
| AD |
=
| 1 |
| 2 |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| b |
=
| 3 |
| 4 |
| a |
| 1 |
| 4 |
| b |
故选:B.
点评:本题考查了平行四边形的性质、向量的平行四边形法则、向量的线性运算,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
复数2+i与复数
在复平面上的对应点分别是A、B,则∠AOB等于( )
| 1 |
| 3+i |
A、
| ||
B、
| ||
C、
| ||
D、
|
若一个正四棱锥的左视图是一个边长为2的正三角形(如图),则该正四棱锥的体积是( )
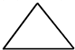

| A、1 | ||||
B、
| ||||
C、
| ||||
D、2
|
已知向量
=(λ,1),
=(λ+2,1),若|
+
|=|
-
|,则实数λ的值为( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、1 | B、2 | C、-1 | D、-2 |
数列{an}满足a1=
,
=
-1(n∈N*),则a10=( )
| 1 |
| 2 |
| 1 |
| an+1-1 |
| 1 |
| an-1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
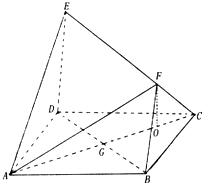 如图正方形ABCD的边长为2
如图正方形ABCD的边长为2