题目内容
设函数f(x),g(x)满足下列条件:(1)f(-1)=-1,f(0)=0,f(1)=1.(2)对任意实数x1,x2都有f(x1)•f(x2)+g(x1)•g(x2)=g(x1-x2),则当n>2,n∈N*时,[f(x)]n+[g(x)]n的最大值为 .
考点:抽象函数及其应用
专题:计算题,函数的性质及应用
分析:由题意,令x2=0得g(x1)=0或g(0)=1,再令x1=-x2=1得g(0)=1;从而令x1=x2得f2(x1)+g2(x1)=1,从而求最大值.
解答:
解:由题意,令x2=0得,
f(x1)•f(0)+g(x1)•g(0)=g(x1),
即g(x1)•g(0)=g(x1),
故g(x1)=0或g(0)=1;
令x1=-x2=1;
则f(1)•f(-1)+g(1)•g(-1)=g(2),
即-1+g(1)•g(-1)=g(2),
故g(x1)=0不成立,
故g(0)=1;
令x1=x2得,
f2(x1)+g2(x1)=1,
故[f(x)]n+[g(x)]n的最大值为1;
故答案为:1.
f(x1)•f(0)+g(x1)•g(0)=g(x1),
即g(x1)•g(0)=g(x1),
故g(x1)=0或g(0)=1;
令x1=-x2=1;
则f(1)•f(-1)+g(1)•g(-1)=g(2),
即-1+g(1)•g(-1)=g(2),
故g(x1)=0不成立,
故g(0)=1;
令x1=x2得,
f2(x1)+g2(x1)=1,
故[f(x)]n+[g(x)]n的最大值为1;
故答案为:1.
点评:本题考查了抽象函数的应用,注意特殊值的应用,属于中档题.

练习册系列答案
相关题目
下列说法不正确的是( )
| A、命题“若x>0且y>0,则x+y>0”的否命题是假命题 | ||
| B、命题“?x0∈R,x02-x0-1<0”的否定是“?x∈R,x2-x-1≥0” | ||
C、“φ=
| ||
| D、a<0时,幂函数y=xa在(0,+∞)上单调递减 |
在平面直角坐标系xOy中,设不等式组
,表示的平面区域为D,在D内任取一整点P(横、纵坐标都是整数)测P落在区域
内的概率为( )
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
将函数y=sin(x+
)cos(x+
)的图象沿x轴向右平移
个单位后,得到一个偶函数的图象,则φ的取值不可能是( )
| φ |
| 2 |
| φ |
| 2 |
| π |
| 8 |
A、
| ||
B、-
| ||
C、
| ||
D、
|
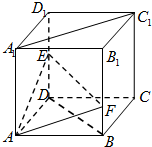 如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,
如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,