Question

如图，在棱长为1的正方体ABCD-A₁B₁C₁D₁中，E是棱BC上的一点，则三棱锥D₁-B₁C₁E的体积等于（　　）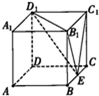

• A、

  1

  3

• B、

  5

  12

• C、

  3

  6

• D、

  1

  6

Answer 1

考点：棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：由VD1-B1C1E=VE-B1D1C1，利用等积法能求出三棱锥D₁-B₁C₁E的体积．

解答： 解：∵在棱长为1的正方体ABCD-A₁B₁C₁D₁中，E是棱BC上的一点，
∴E到平面B₁D₁C₁的距离h=1，
S△B1D1C1=

1

2

×1×1=

1

2

，
∴VD1-B1C1E=VE-B1D1C1=

1

3

•S△B1D1C1•h=

1

3

×

1

2

×1=

1

6

．
故选：D．

点评：本题考查三棱锥的体积的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．