题目内容
对于函数f(x),若在其定义域内存在两个实数a,b(a<b),使当x∈[a,b]时,f(x)的值域是[2a,2b],则称f(x)为“快乐函数”…是否存在实数m,当a+b≤4时,使函数f(x)=x2-4x+m,x∈[0,+∞﹚为“快乐函数”.若存在,求出m的范围,若不存在,说明理由.
考点:函数的值域
专题:计算题,函数的性质及应用
分析:首先要理解快乐函数的定义,其次要注意二次函数的对称轴及给出的a、b的条件,结合条件进行讨论函数的最值,从而解m.
解答:
解:∵x∈[a,b]且a+b≤4,函数f(x)=x2-4x+m的对称轴为x=2,
∴a≤2,b与2的大小关系不确定,函数f(x)在[a,b]上的最大值为f﹙a﹚=a2-4a+m;
又∵值域为[2a,2b];
①若b≤2,则f﹙a﹚=a2-4a+m=2b;f﹙b﹚=b2-4b+m=2a;
消去m得a2-b2-2a+2b=0,
∴﹙a-b﹚﹙a+b-2﹚=0
∵a>b,a≠b,
∴a+b=2,b>1
∴a=2-b代入b2-4b+m=2a,
﹙b-1﹚2=5-m,
∴0<5-m≤1,
即4≤m<5,
②若b>2,则f﹙a﹚=a2-4a+m=2b;f﹙2﹚=4-8+m=2a,
即(a-2)2=2(b-a)>0,
∴a<2,
∴m=2a+4<8,
综上所述,m<8.
∴a≤2,b与2的大小关系不确定,函数f(x)在[a,b]上的最大值为f﹙a﹚=a2-4a+m;
又∵值域为[2a,2b];
①若b≤2,则f﹙a﹚=a2-4a+m=2b;f﹙b﹚=b2-4b+m=2a;
消去m得a2-b2-2a+2b=0,
∴﹙a-b﹚﹙a+b-2﹚=0
∵a>b,a≠b,
∴a+b=2,b>1
∴a=2-b代入b2-4b+m=2a,
﹙b-1﹚2=5-m,
∴0<5-m≤1,
即4≤m<5,
②若b>2,则f﹙a﹚=a2-4a+m=2b;f﹙2﹚=4-8+m=2a,
即(a-2)2=2(b-a)>0,
∴a<2,
∴m=2a+4<8,
综上所述,m<8.
点评:本题考查了学生对新定义的接受能力及二次函数的最值与值域问题的处理方法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设i是虚数单位,复数Z=
,则
=( )
| 2 |
| 1+i |
| Z |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
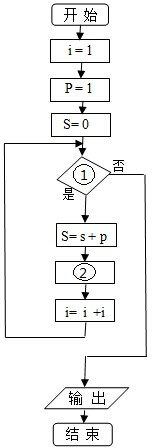 给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.先将下面给出的程序框图补充完整,再根据程序框图写出程序.
给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.先将下面给出的程序框图补充完整,再根据程序框图写出程序.