题目内容
已知函数f(x)=
在[2,+∞)上是单调递增,则a的取值范围是 .
| x2-ax+3a |
考点:函数单调性的性质
专题:函数的性质及应用
分析:令g(x)=x2-ax+3a,若函数f(x)=
在[2,+∞)上是单调递增,则函数g(x)在区间[2,+∞)内单调递增,且恒大于等于0,进而得到a的取值范围.
| x2-ax+3a |
解答:
解:令g(x)=x2-ax+3a,
∵函数f(x)=
在[2,+∞)上是单调递增,
∴函数g(x)在区间[2,+∞)内单调递增,且恒大于等于0
∴
a≤2且g(2)≥0
∴a≤4且4+a≥0
∴-4≤a≤4
故答案为:-4≤a≤4
∵函数f(x)=
| x2-ax+3a |
∴函数g(x)在区间[2,+∞)内单调递增,且恒大于等于0
∴
| 1 |
| 2 |
∴a≤4且4+a≥0
∴-4≤a≤4
故答案为:-4≤a≤4
点评:本题考查的知识点是函数的单调性,其中根据复合函数的单调性和函数有意义的原则,得到函数g(x)=x2-ax+3a,在区间[2,+∞)内单调递增,且恒大于等于0,是解答的关键.

练习册系列答案
相关题目
双曲线x2-3y2=-1的渐近线的倾斜角为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
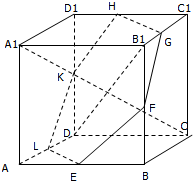 如图所示正方体ABCD-A1B1C1D1中,E、F、G、H、K、L分别为AB、BB1、B1C1、C1D1、D1D、DA的中点,求DB1与平面EFGHKL所成角的余弦值.
如图所示正方体ABCD-A1B1C1D1中,E、F、G、H、K、L分别为AB、BB1、B1C1、C1D1、D1D、DA的中点,求DB1与平面EFGHKL所成角的余弦值.