题目内容
10．某几何体的三视图如图，则该几何体的体积为（ ）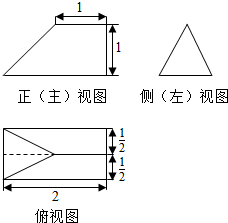
| A． | $\frac{5}{6}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{3}$ |
分析 几何体为三棱柱切去一个三棱锥得到的，使用作差法求出几何体体积．
解答 
解：由三视图可知几何体为直三棱柱ABC-A′B′C′切去三棱锥D-A′B′C′得到的几何体．
其中棱柱的底面ABC中，AB=1，AB边上的高为1，棱柱的高为2，切去三棱锥的高为1，
∴几何体的体积V=$\frac{1}{2}×1×1×2$-$\frac{1}{3}×\frac{1}{2}×1×1×1$=$\frac{5}{6}$．
故选：A．
点评 本题考查了空间几何体的结构特征和三视图，体积计算，属于基础题．
练习册系列答案
相关题目
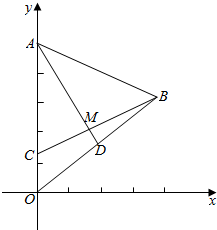如图所示，已知△AOB中，A（0，5），O（0，0），B（4，3），$\overrightarrow{OC}$=$\frac{1}{4}$$\overrightarrow{OA}$，$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OB}$，AD与BC相交于点M，求点M的坐标．