题目内容
9.已知函数f(x)=x-alnx在区间(0,2]上单调递减,则实数a的取值范围是( )| A. | (0,$\frac{1}{2}$) | B. | (0,2) | C. | ($\frac{1}{2}$,+∞) | D. | [2,+∞) |
分析 利用函数单调和导数之间的关系转化为f′(x)≤0恒成立,利用参数分离法进行求解即可.
解答 解:函数的导数为f′(x)=1-$\frac{a}{x}$,
若函数f(x)=x-alnx在区间(0,2]上单调递减,
则等价为f′(x)≤0恒成立,
即1-$\frac{a}{x}$≤0,即$\frac{a}{x}$≥1,即a≥x,
∵0<x≤2,
∴a≥2,
故选:D
点评 本题主要考查函数单调性和导数的关系,利用参数分离法是解决本题的关键.比较基础.

练习册系列答案
相关题目
17.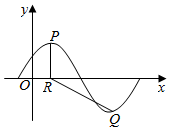 如图所示为f(x)=Asin($\frac{π}{6}$x+φ)(A>0,0<φ<$\frac{π}{2}$)的部分图象,P,Q分别为f(x)图象的最高点和最低点,点P坐标为(2,A),PR⊥x轴于R,若∠PRQ=$\frac{2π}{3}$.则A及φ的值分别是( )
如图所示为f(x)=Asin($\frac{π}{6}$x+φ)(A>0,0<φ<$\frac{π}{2}$)的部分图象,P,Q分别为f(x)图象的最高点和最低点,点P坐标为(2,A),PR⊥x轴于R,若∠PRQ=$\frac{2π}{3}$.则A及φ的值分别是( )
 如图所示为f(x)=Asin($\frac{π}{6}$x+φ)(A>0,0<φ<$\frac{π}{2}$)的部分图象,P,Q分别为f(x)图象的最高点和最低点,点P坐标为(2,A),PR⊥x轴于R,若∠PRQ=$\frac{2π}{3}$.则A及φ的值分别是( )
如图所示为f(x)=Asin($\frac{π}{6}$x+φ)(A>0,0<φ<$\frac{π}{2}$)的部分图象,P,Q分别为f(x)图象的最高点和最低点,点P坐标为(2,A),PR⊥x轴于R,若∠PRQ=$\frac{2π}{3}$.则A及φ的值分别是( )| A. | $\sqrt{3}$,$\frac{π}{6}$ | B. | $\sqrt{3}$,$\frac{π}{3}$ | C. | 2$\sqrt{3}$,$\frac{π}{6}$ | D. | 2$\sqrt{3}$,$\frac{π}{3}$ |
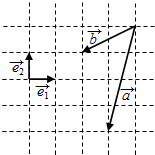 向量$\overrightarrow{e_1},\;\overrightarrow{e_2},\;\overrightarrow a,\;\overrightarrow b$在正方形网格中的位置如图所示,若$\overrightarrow a-\overrightarrow b=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,则x=1,y=-3.
向量$\overrightarrow{e_1},\;\overrightarrow{e_2},\;\overrightarrow a,\;\overrightarrow b$在正方形网格中的位置如图所示,若$\overrightarrow a-\overrightarrow b=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,则x=1,y=-3. 一半径为4m的水轮,如图所示水轮圆心O距离水面2m,己知水轮每分钟转动4圈,如果当水轮上P点从水中浮现时(图中P0)点开始计算时间.
一半径为4m的水轮,如图所示水轮圆心O距离水面2m,己知水轮每分钟转动4圈,如果当水轮上P点从水中浮现时(图中P0)点开始计算时间.