题目内容
10.已知点A(1,0),点P是圆C:(x+1)2+y2=8上的任意一点,线段PA的垂直平分线与直线CP交于点E.(1)求点E的轨迹方程;
(2)若直线l与点E的轨迹有两个不同的交点M和N,问点E的轨迹的右焦点F是否可以为△BMN的垂心?其中B为上顶点.若可以,求出直线l的方程;若不可以,请说明理由.
分析 (1)由题意画出图形,然后利用椭圆定义可得点E的轨迹为焦点在x轴上,2a=$2\sqrt{2}$,2c=2的椭圆,结合隐含条件求出b后可得椭圆方程;
(2)假设右焦点F为△BMN的垂心,由F(1,0),可得直线BF的斜率为-1,从而直线l的斜率为1,设其方程为y=x+m.联立直线方程和椭圆方程,化为关于x的一元二次方程,求出M,N的横坐标的和与积,再由$\overrightarrow{NF}•\overrightarrow{MB}=0$求得k值得答案.
解答 解:(1)如图,由题意可得|EC|+|EA|=|EC|+|EP|=$2\sqrt{2}$>|AC|=2,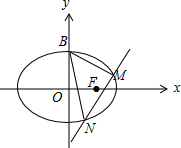
则由椭圆的定义可知点E的轨迹为焦点在x轴上,2a=$2\sqrt{2}$,2c=2的椭圆,
∴$a=\sqrt{2},c=1,b=1$,
则椭圆E的轨迹方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)假设右焦点F为△BMN的垂心,
∵F(1,0),∴直线BF的斜率为-1,从而直线l的斜率为1,设其方程为y=x+m.
联立$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,得3x2+4mx+2m2-2=0.
由△=16m2-24(m2-1)=24-8m2>0,得m2<3.
设M(x1,y1),N(x2,y2),则${x}_{1}+{x}_{2}=-\frac{4}{3}m,{x}_{1}{x}_{2}=\frac{2{m}^{2}-2}{3}$.
于是$\overrightarrow{NF}•\overrightarrow{BM}=(1-{x}_{2}){x}_{1}-{y}_{2}({y}_{1}-1)$=x1+y2-x1x2-y1y2=x1+x2+m-x1x2-(x1+m)(x2+m)
=$-2{x}_{1}{x}_{2}+(1-m)({x}_{1}+{x}_{2})+m-{m}^{2}$=$-2•\frac{2{m}^{2}-2}{3}+(1-m)•(-\frac{4m}{3})+m-{m}^{2}$=$-{m}^{2}-\frac{1}{3}m+\frac{4}{3}=0$,
解得m=1或m=$-\frac{4}{3}$.
当m=1时,点B即为直线l与椭圆的交点,不合题意;
当m=-$\frac{4}{3}$时,经检验直线l和椭圆相交,符合题意.
∴当且仅当直线l的方程为y=x-$\frac{4}{3}$时,点F是△BMN的垂心.
点评 本题考查利用椭圆的定义求椭圆的方程,考查了直线与圆锥曲线位置关系的应用,训练了利用向量数量积判断两直线的垂直关系,是中档题.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案| A. | 540 | B. | 240 | C. | 180 | D. | 150 |
| A. | $\sqrt{2}$-1 | B. | $\sqrt{3}$-1 | C. | $\frac{{\sqrt{2}-1}}{2}$ | D. | $\frac{{\sqrt{3}-1}}{3}$ |
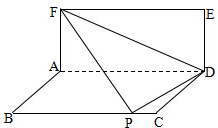 已知两矩形ABCD与ADEF所在的平面互相垂直,AB=1,若将△DEF沿直线FD翻折,使得点E落在边BC上(即点P),则当AD取最小值时,边AF的长是$\sqrt{2}$;此时四面体F-ADP的外接球的半径是$\frac{\sqrt{6}}{2}$.
已知两矩形ABCD与ADEF所在的平面互相垂直,AB=1,若将△DEF沿直线FD翻折,使得点E落在边BC上(即点P),则当AD取最小值时,边AF的长是$\sqrt{2}$;此时四面体F-ADP的外接球的半径是$\frac{\sqrt{6}}{2}$.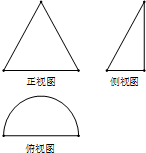 某几何体的三视图如图所示,其中正视图是腰长为2cm的等腰三角形,俯视图是半径为1cm的半圆,则该几何体的表面积是$\frac{3π}{2}$+$\sqrt{3}$cm2,体积是$\frac{\sqrt{3}}{6}$πcm3.
某几何体的三视图如图所示,其中正视图是腰长为2cm的等腰三角形,俯视图是半径为1cm的半圆,则该几何体的表面积是$\frac{3π}{2}$+$\sqrt{3}$cm2,体积是$\frac{\sqrt{3}}{6}$πcm3.