题目内容
15.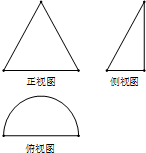 某几何体的三视图如图所示,其中正视图是腰长为2cm的等腰三角形,俯视图是半径为1cm的半圆,则该几何体的表面积是$\frac{3π}{2}$+$\sqrt{3}$cm2,体积是$\frac{\sqrt{3}}{6}$πcm3.
某几何体的三视图如图所示,其中正视图是腰长为2cm的等腰三角形,俯视图是半径为1cm的半圆,则该几何体的表面积是$\frac{3π}{2}$+$\sqrt{3}$cm2,体积是$\frac{\sqrt{3}}{6}$πcm3.
分析 根据几何体的三视图得出该几何体是底面为半圆的圆锥体的一部分,结合图中数据即可求出几何体的表面积与体积.
解答 解:根据几何体的三视图知,该几何体是底面为半圆的圆锥体的一部分,
且母线长为2cm,底面圆半径为1cm,
则该几何体的表面积是
S=S底+S侧+S△=$\frac{1}{2}$π•12+$\frac{1}{2}$π•1•2+$\frac{\sqrt{3}}{4}$•22=($\frac{3π}{2}$+$\sqrt{3}$)cm2,
体积是V=$\frac{1}{2}$•$\frac{1}{3}$π•12•$\sqrt{{2}^{2}{-1}^{2}}$=$\frac{\sqrt{3}}{6}$π(cm3).
故答案为:$\frac{3}{2}π+\sqrt{3}$;$\frac{{\sqrt{3}}}{6}π$.
点评 本题考查了利用三视图求几何体的表面积与体积的应用问题,是基础题目.

练习册系列答案
相关题目
5.若集合A={x|y=lgx},B={x|y=$\sqrt{1-x}$},则A∩B等于( )
| A. | [0,1] | B. | (0,1] | C. | [1,+∞) | D. | (-∞,1] |
6.椭圆的四个顶点A,B,C,D构成四边形为菱形,若菱形ABCD的内切圆恰好过焦点,则椭圆离心率为( )
| A. | $\frac{3\sqrt{5}}{2}$ | B. | $\frac{3+\sqrt{5}}{8}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{5}+1}{4}$ |
3.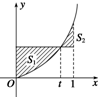 在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为( )
在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为( )
 在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为( )
在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为( )| A. | ($\frac{1}{2}$,1) | B. | ($\frac{1}{2}$,2] | C. | [0,1] | D. | (1,2] |
4.已知集合A={x|x2-4=0},B={1,2},则A∩B=( )
| A. | 2 | B. | {-2,2} | C. | {2} | D. | ∅ |
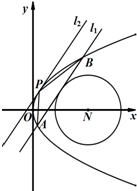 设抛物线C:y2=2px(p>0)的焦点为F,抛物线C上点M(3,y0)满足|MF|=4.
设抛物线C:y2=2px(p>0)的焦点为F,抛物线C上点M(3,y0)满足|MF|=4.