题目内容

18．某机构邀请5位市民体验“刷卡支付”、“微信支付”、“支付宝支付”，每人限使用一种支付方式，每种支付方式都要有人选择，则不同的支付方式种数有（　　）
A．540B．240C．180D．150

分析 ①、先将5位市民分成3组，②、将分好的三组，对应3种支付方式，由分步计数原理计算可得．

解答 解：①、先将5位市民分成3组，
若分为2、2、1的三组，有$\frac{{C}_{5}^{2}•{C}_{3}^{2}}{{A}_{2}^{2}}$=15种情况，
若分为3、1、1的三组，有C53=10种情况，
共有15+10=25种分组方法，
②、将分好的三组，对应3种支付方式，有A33=6种情况，
则每种支付方式都要有人选择，则不同的支付方式有25×6=150种情况，
故选：D．

点评 本题考查了分组分配的问题，关键是分组，属于中档题．

练习册系列答案
相关题目
8．（x2-x+ay）7的展开式中，x7y2的系数为-$\frac{105}{2}$，则a等于（　　）
A．-2B．$\frac{1}{2}$C．±2D．±$\frac{1}{2}$
9．已知a，b，c分别是△ABC的内角A，B，C的对边，且c=2，C=$\frac{π}{3}$．
（Ⅰ）若△ABC的面积等于$\sqrt{3}$，求a，b；
（Ⅱ）若sinC+sin（B-A）=2sin2A，求锐角A的值．
6．椭圆的四个顶点A，B，C，D构成四边形为菱形，若菱形ABCD的内切圆恰好过焦点，则椭圆离心率为（　　）
A．$\frac{3\sqrt{5}}{2}$B．$\frac{3+\sqrt{5}}{8}$C．$\frac{\sqrt{5}-1}{2}$D．$\frac{\sqrt{5}+1}{4}$
13．与直线2x+y+1=0垂直，且交点在y轴上的直线方程为x-2y-2=0（要求写一般式）．
3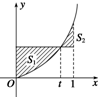．在区间[0，1]上给定曲线y=x2，如图所示，0＜t＜1，S1，S2是t的函数，则函数g（t）=S1+S2的单调递增区间为（　　）
A．（$\frac{1}{2}$，1）B．（$\frac{1}{2}$，2]C．[0，1]D．（1，2]
10．已知点A（1，0），点P是圆C：（x+1）2+y2=8上的任意一点，线段PA的垂直平分线与直线CP交于点E．
（1）求点E的轨迹方程；
（2）若直线l与点E的轨迹有两个不同的交点M和N，问点E的轨迹的右焦点F是否可以为△BMN的垂心？其中B为上顶点．若可以，求出直线l的方程；若不可以，请说明理由．
7．已知函数f（x）=sinxcosx-$\sqrt{3}$cos2x．
（Ⅰ）求f（x）的最小正周期；
（Ⅱ）在△ABC中，内角A，B，C的对边分别为a，b，c，且（a+c）（sinA-sinC）=b（sinA-sinB），求f（A）的取值范围．
8．若直线（1+a）x+y+1=0与圆（x-1）2+y2=1相切，则a的值为（　　）
A．1，-1B．2，-2C．1D．-1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网