题目内容
5.f(x)是定义在非零实数集上的函数,f′(x)为其导函数,且x>0时,xf′(x)-f(x)<0,记a=$\frac{f({2}^{0.2})}{{2}^{0.2}}$,b=$\frac{f(0.{2}^{2})}{0.{2}^{2}}$,c=$\frac{f(lo{g}_{2}5)}{lo{g}_{2}5}$,则a,b,c的大小关系为c<a<b.分析 令g(x)=$\frac{f(x)}{x}$,得到g(x)在(0,+∞)递减,通过${log}_{2}^{5}$>20.2>0.22,从而得出答案
解答 解:令g(x)=$\frac{f(x)}{x}$,则g′(x)=$\frac{xf′(x)-f(x)}{{x}^{2}}$,
∵x>0时,xf′(x)-f(x)<0,
∴g(x)在(0,+∞)递减,
又${log}_{2}^{5}$>${log}_{2}^{4}$=2,1<20.2<2,0.22=0.04,
∴${log}_{2}^{5}$>20.2>0.22,
∴g(${log}_{2}^{5}$)<g(20.2)<g(0.22),
∴c<a<b,
故答案为:c<a<b.
点评 本题考查了函数的单调性问题,考查了导数的应用,考查了指数,对数的性质,是一道中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
15.在平面直角坐标系中,过(1,0)点且倾率为-1的直线不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.△ABC的三个内角A,B,C所对边的长分别为a,b,c,设向量$\overrightarrow{p}$=(a+c,b),$\overrightarrow{q}$=(b,c-a).若$\overrightarrow{p}$∥$\overrightarrow{q}$,则角C的大小为( )
| A. | $\frac{π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{3}$ |
15.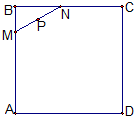 正方形ABCD的边长为2,(如图),线段MN=1,当点M、N在正方形ABCD的边上滑动一周(保持MN的长度不变)时,线段MN的中点P的轨迹围成一个封闭图形E,现向正方形中随机投入一点,则该点落在E内的概率是( )
正方形ABCD的边长为2,(如图),线段MN=1,当点M、N在正方形ABCD的边上滑动一周(保持MN的长度不变)时,线段MN的中点P的轨迹围成一个封闭图形E,现向正方形中随机投入一点,则该点落在E内的概率是( )
 正方形ABCD的边长为2,(如图),线段MN=1,当点M、N在正方形ABCD的边上滑动一周(保持MN的长度不变)时,线段MN的中点P的轨迹围成一个封闭图形E,现向正方形中随机投入一点,则该点落在E内的概率是( )
正方形ABCD的边长为2,(如图),线段MN=1,当点M、N在正方形ABCD的边上滑动一周(保持MN的长度不变)时,线段MN的中点P的轨迹围成一个封闭图形E,现向正方形中随机投入一点,则该点落在E内的概率是( )| A. | $\frac{7}{8}$ | B. | $\frac{π}{16}$ | C. | $1-\frac{π}{16}$ | D. | $\frac{3}{4}+\frac{π}{16}$ |
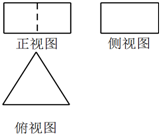 如图为某几何体的三视图,其中俯视图为边长为2的正三角形,正视图为长为2,宽为1的矩形,则该三视图的体积为$\sqrt{3}$,表面积为$6+2\sqrt{3}$.
如图为某几何体的三视图,其中俯视图为边长为2的正三角形,正视图为长为2,宽为1的矩形,则该三视图的体积为$\sqrt{3}$,表面积为$6+2\sqrt{3}$.