题目内容
F1,F2是双曲线C:
-
=1(a>0,b>0)的左右焦点,过F1的直线l与C的左右两支分别交于AB两点,若BF2⊥AB,且线段AB,BF2,AF2长度成等差数列,则e= .
| x2 |
| a2 |
| y2 |
| b2 |
考点:双曲线的简单性质
专题:等差数列与等比数列,圆锥曲线的定义、性质与方程
分析:运用双曲线的定义和等差数列的性质,计算即可得到|BF2|=4a,再在直角三角形BF1F2中,运用勾股定理,结合离心率公式,计算即可得到.
解答:
解: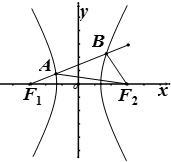 设|BF2|=n,
设|BF2|=n,
由双曲线的定义可得,|BF1|=|BF2|+2a=n+2a,
设|AF2|=m,由线段AB,BF2,AF2长度成等差数列,
即有2|BF2|=|AB|+|AF2|,
即为2n=|AB|+m,
即|AB|=2n-m,
由双曲线的定义可得,|AF1|=|AF2|-2a=m-2a,
即有|BF1|=|AB|+|AF1|=2n-2a,
则2n-2a=n+2a,即为n=4a,
在直角三角形BF1F2中,
|F1F2|2=|BF1|2+|BF2|2,
即有4c2=(2n-2a)2+n2=(6a)2+16a2,
即有c2=13a2,
即离心率e=
=
.
故答案为:
.
 设|BF2|=n,
设|BF2|=n,由双曲线的定义可得,|BF1|=|BF2|+2a=n+2a,
设|AF2|=m,由线段AB,BF2,AF2长度成等差数列,
即有2|BF2|=|AB|+|AF2|,
即为2n=|AB|+m,
即|AB|=2n-m,
由双曲线的定义可得,|AF1|=|AF2|-2a=m-2a,
即有|BF1|=|AB|+|AF1|=2n-2a,
则2n-2a=n+2a,即为n=4a,
在直角三角形BF1F2中,
|F1F2|2=|BF1|2+|BF2|2,
即有4c2=(2n-2a)2+n2=(6a)2+16a2,
即有c2=13a2,
即离心率e=
| c |
| a |
| 13 |
故答案为:
| 13 |
点评:本题考查双曲线的定义和性质,主要考查离心率的求法,同时考查等差数列的性质,运用双曲线的定义和勾股定理是解题的关键,属于中档题.

练习册系列答案
相关题目
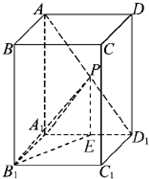
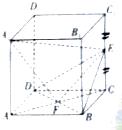 如图,正方体ABCD-A1B1C1D1中,E是CC1的中点,F是AC与BD的交点.
如图,正方体ABCD-A1B1C1D1中,E是CC1的中点,F是AC与BD的交点. 给出下列四个结论:
给出下列四个结论: