题目内容
如图,已知ABCD-A1B1C1D1是底面为正方形的长方体,A1D1=2,A1A=2
,点P为动点,
(1)当P为AD1得中点时,求异面直线AA1与B1P所成角的余弦值;
(2)当PB1与平面AA1D1所成角的正切值的最大值.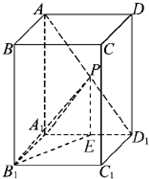
| 3 |
(1)当P为AD1得中点时,求异面直线AA1与B1P所成角的余弦值;
(2)当PB1与平面AA1D1所成角的正切值的最大值.

考点:直线与平面所成的角,异面直线及其所成的角
专题:空间角
分析:(1)过点P作PE⊥A1D1,垂足为E,连接B1E,则PE∥AA1,可得∠B1PE是异面直线AA1与B1P所成的角,在Rt△B1PE中,利用余弦函数可求异面异面直线AA1与B1P所成角的余弦值.
(2)由(1)知,B1A1⊥平面AA1D1,故∠B1PA1是PB1与平面AA1D1所成的角且tan∠B1PA1=
=
,当A1P最小时,tan∠B1PA1最大,由此可得结论.
(2)由(1)知,B1A1⊥平面AA1D1,故∠B1PA1是PB1与平面AA1D1所成的角且tan∠B1PA1=
| B1A1 |
| A1P |
| 2 |
| A1P |
解答:
解:(1)过点P作PE⊥A1D1,垂足为E,连接B1E(如图),
则PE∥AA1, ∴∠B1PE是异面直线AA1与B1P所成的角.
∴∠B1PE是异面直线AA1与B1P所成的角.
ABCD-A1B1C1D1是底面为正方形的长方体,A1D1=2,A1A=2
,
∴A1B1=A1D1=2,A1E=
A1D1=1.
又PE=
AA1=
.
∴在Rt△B1PE中,B1P=
=2
,
cos∠B1PE=
=
=
.
∴异面异面直线AA1与B1P所成角的余弦值为
.
(2)由(1)知,B1A1⊥平面AA1D1,
∴∠B1PA1是PB1与平面AA1D1所成的角,
且tan∠B1PA1=
=
,
当A1P最小时,tan∠B1PA1最大,
这时A1P⊥AD1,由A1P=
=
,
得tan∠B1PA1=
,
即PB1与平面AA1D1所成角的正切值的最大值为
.
则PE∥AA1,
 ∴∠B1PE是异面直线AA1与B1P所成的角.
∴∠B1PE是异面直线AA1与B1P所成的角.ABCD-A1B1C1D1是底面为正方形的长方体,A1D1=2,A1A=2
| 3 |
∴A1B1=A1D1=2,A1E=
| 1 |
| 2 |
又PE=
| 1 |
| 2 |
| 3 |
∴在Rt△B1PE中,B1P=
| 5+3 |
| 2 |
cos∠B1PE=
| PE |
| B1P |
| ||
2
|
| ||
| 4 |
∴异面异面直线AA1与B1P所成角的余弦值为
| ||
| 4 |
(2)由(1)知,B1A1⊥平面AA1D1,
∴∠B1PA1是PB1与平面AA1D1所成的角,
且tan∠B1PA1=
| B1A1 |
| A1P |
| 2 |
| A1P |
当A1P最小时,tan∠B1PA1最大,
这时A1P⊥AD1,由A1P=
| A1D1•A1A |
| AD1 |
| 3 |
得tan∠B1PA1=
2
| ||
| 3 |
即PB1与平面AA1D1所成角的正切值的最大值为
2
| ||
| 3 |
点评:本题考查线线角、线面角的求法,解题的关键是正确作出线线角与线面角,注意空间思维能力的培养,属于中档题.

练习册系列答案
相关题目
已知a∈R,b∈R+,e为自然数的底数,则[
ea-ln(2b)]2+(a-b)2的最小值为( )
| 1 |
| 2 |
| A、(1-ln2)2 | ||
| B、2(1-ln2)2 | ||
| C、1+ln2 | ||
D、
|
已知四面体OABC各棱长为1,D是棱OA的中点,则异面直线BD与AC所成角的余弦值( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
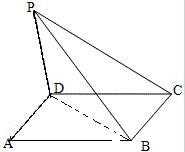 如图,PD⊥平面ABCD,AD⊥PC,AD∥BC,PD:DC:BC=1:1:
如图,PD⊥平面ABCD,AD⊥PC,AD∥BC,PD:DC:BC=1:1: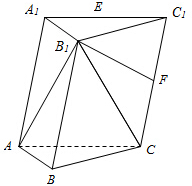 已知三棱柱ABC-A1B1C1中,△ABC是以AC为斜边的等腰直角三角形,且B1A=B1C=B1B=AC=2.
已知三棱柱ABC-A1B1C1中,△ABC是以AC为斜边的等腰直角三角形,且B1A=B1C=B1B=AC=2.