题目内容
 给出下列四个结论:
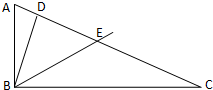
给出下列四个结论:(1)如图Rt△ABC中,|AC|=2,∠B=90°,∠C=30°.D是斜边AC上的点,|CD|=|CB|.以B为起点任作一条射线BE交AC于E点,则E点落在线段CD上的概率是
| ||
| 2 |
(2)设某大学的女生体重y(kg)与身高x(cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的线性回归方程为
 |
| y |
(3)为调查中学生近视情况,测得某校男生150名中有80名近视,在140名女生中有70名近视.在检验这些学生眼睛近视是否与性别有关时,应该用独立性检验最有说服力;
(4)已知随机变量ξ服从正态分布N(1,σ2),P(ξ≤4)=0.79,则P(ξ≤-2)=0.21;其中正确结论的个数为( )
| A、1 | B、2 | C、3 | D、4 |
考点:两个变量的线性相关,正态分布曲线的特点及曲线所表示的意义
专题:综合题,概率与统计
分析:对四个命题分别进行判断,即可得出结论.
解答:
解:(1)由题意,|CD|=|CB|,∠C=30°,所以∠CBD=75°,所以E点落在线段CD上的概率是
=
,故不正确;
(2)设某大学的女生体重y(kg)与身高x(cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的线性回归方程为
=0.85x-85.71,则若该大学某女生身高增加1cm,则其体重约增加0.85kg,正确;
(3)为调查中学生近视情况,测得某校男生150名中有80名近视,在140名女生中有70名近视.在检验这些学生眼睛近视是否与性别有关时,应该用独立性检验最有说服力,正确;
(4)已知随机变量ξ服从正态分布N(1,σ2),图象关于x=1对称,因为P(ξ≤4)=0.79,则P(ξ≤-2)=0.21,正确;
故正确结论的个数为3,
故选:C.
| 75 |
| 90 |
| 5 |
| 6 |
(2)设某大学的女生体重y(kg)与身高x(cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的线性回归方程为
 |
| y |
(3)为调查中学生近视情况,测得某校男生150名中有80名近视,在140名女生中有70名近视.在检验这些学生眼睛近视是否与性别有关时,应该用独立性检验最有说服力,正确;
(4)已知随机变量ξ服从正态分布N(1,σ2),图象关于x=1对称,因为P(ξ≤4)=0.79,则P(ξ≤-2)=0.21,正确;
故正确结论的个数为3,
故选:C.
点评:本题考查命题的真假的判断,考查学生分析解决问题的能力,综合性强.

练习册系列答案
相关题目
已知
,
是两个不共线的向量,向量
=
+sina•
(-
<a<
),
=2
-
,
=3
-
,若A,B,C三点共线,且函数f(x-a)=4cos(x-a)cos(x-2a),则f(x)在[-
,
]上的值域为( )
| e1 |
| e2 |
| PA |
| e1 |
| e2 |
| π |
| 2 |
| π |
| 2 |
| PB |
| e1 |
| e2 |
| PC |
| e1 |
| 5 |
| 2 |
| e2 |
| π |
| 4 |
| π |
| 6 |
A、[-2,
| ||||
B、[1-
| ||||
C、[-2
| ||||
D、[
|
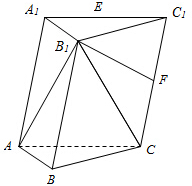 已知三棱柱ABC-A1B1C1中,△ABC是以AC为斜边的等腰直角三角形,且B1A=B1C=B1B=AC=2.
已知三棱柱ABC-A1B1C1中,△ABC是以AC为斜边的等腰直角三角形,且B1A=B1C=B1B=AC=2.