题目内容
设空间任意一点O和不共线三点A、B、C,若点P满足向量关系
=x
-
+3
,且P、A、B、C四点共面,则x= .
| OP |
| OA |
| OB |
| OC |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:利用空间向量四点共面基本定理即可得出.
解答:
解:∵空间任意一点O和不共线三点A、B、C,点P满足向量关系
=x
-
+3
,且P、A、B、C四点共面,
则x-1+3=1,解得x=-1.
故答案为:-1.
| OP |
| OA |
| OB |
| OC |
则x-1+3=1,解得x=-1.
故答案为:-1.
点评:本题考查了空间向量四点共面基本定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知正方形ABCD的边长为2,P是平面ABCD外一点,且PA=PB=PC=PD=2
,则PA与平面ABCD所成的角是( )
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
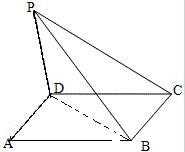 如图,PD⊥平面ABCD,AD⊥PC,AD∥BC,PD:DC:BC=1:1:
如图,PD⊥平面ABCD,AD⊥PC,AD∥BC,PD:DC:BC=1:1: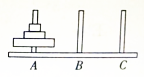 从古印度的汉诺塔传说演变了一个汉诺塔游戏:如图,有三根杆子A、B、C,A杆上有三个碟子(大小不等,自上到下,由小到大),每次移动一个碟子,小的只能叠在大的上面,把所有的碟子从A杆移到C杆上,试设计一个算法,完成上述游戏.
从古印度的汉诺塔传说演变了一个汉诺塔游戏:如图,有三根杆子A、B、C,A杆上有三个碟子(大小不等,自上到下,由小到大),每次移动一个碟子,小的只能叠在大的上面,把所有的碟子从A杆移到C杆上,试设计一个算法,完成上述游戏.