题目内容
(1)已知a,b∈R*,a+b=4,求证:
+
≥1.
(2)已知a,b,c∈R*,a+b+c=9,求证:
+
+
≥1.
并类比上面的结论写出推广后的一般性结论.(不需证明)
| 1 |
| a |
| 1 |
| b |
(2)已知a,b,c∈R*,a+b+c=9,求证:
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
并类比上面的结论写出推广后的一般性结论.(不需证明)
考点:不等式的证明
专题:不等式的解法及应用
分析:(1)根据基本不等式的性质,即可证明不等式
+
≥1.
(2)根据基本不等式,结合类比即可得到结论.
| 1 |
| a |
| 1 |
| b |
(2)根据基本不等式,结合类比即可得到结论.
解答:
解:(1)∵a+b=4,∴
+
=1,则
+
=(
+
)(
+
)=
+
+
+
≥
+2
=
+
=1,
当且仅当
=
,即a=b=2时,取等号.∴
+
≥1.
2)由柯西不等式(a+b+c)(
+
+
)≥(1+1+1)2,
+
+
≥1,
结论推广为:a1+a2+…+an=n2,则
+
+…+
≥1.
| a |
| 4 |
| b |
| 4 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| a |
| 4 |
| b |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| b |
| 4a |
| a |
| 4b |
| 1 |
| 2 |
|
| 1 |
| 2 |
| 1 |
| 2 |
当且仅当
| b |
| 4a |
| a |
| 4b |
| 1 |
| a |
| 1 |
| b |
2)由柯西不等式(a+b+c)(
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
结论推广为:a1+a2+…+an=n2,则
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
点评:本题忽悠考查基本不等式的应用,注意基本不等式成立的条件.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
若实数x为10和90的等差中项,则x的值为( )
| A、30 | B、40 | C、50 | D、60 |
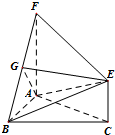 如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF
如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF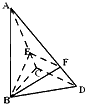 已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且
已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且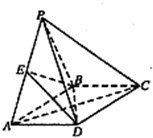 如图,四棱锥P-ABCD的底面ABCD是矩形,侧面PAB是正三角形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,侧面PAB是正三角形,AB=2,