题目内容
已知x为实数,复数z=(x2+x-2)+(x2+3x+2)i.
(Ⅰ)当x为何值时,复数z为纯虚数?
(Ⅱ)当x=0时,复数z在复平面内对应的点Z落在直线y=-mx+n上,其中mn>0,求
+
的最小值及取得最值时的m、n值.
(Ⅰ)当x为何值时,复数z为纯虚数?
(Ⅱ)当x=0时,复数z在复平面内对应的点Z落在直线y=-mx+n上,其中mn>0,求
| 1 |
| m |
| 1 |
| n |
考点:复数的基本概念,基本不等式
专题:数系的扩充和复数
分析:(Ⅰ)复数z为纯虚数,复数的实部为0,虚部不为0,求出x即可;
(Ⅱ)当x=0时,求出m、n的关系,其中mn>0,利用基本不等式求
+
的最小值及取得最值时的m、n值.
(Ⅱ)当x=0时,求出m、n的关系,其中mn>0,利用基本不等式求
| 1 |
| m |
| 1 |
| n |
解答:
解:(Ⅰ)复数z为纯虚数,∴
,解得x=1.
(Ⅱ)当x=0时,复数z(-2,2),复数z在复平面内对应的点Z落在直线y=-mx+n上,∴2m+n=2,
∵mn>0,∴
+
=(
+
)(m+
)=
+
+
≥
+
当且仅当n2=2m2等号成立,
又2m+n=2,
∴m=2-
,n=2
-2.
|
(Ⅱ)当x=0时,复数z(-2,2),复数z在复平面内对应的点Z落在直线y=-mx+n上,∴2m+n=2,
∵mn>0,∴
| 1 |
| m |
| 1 |
| n |
| 1 |
| m |
| 1 |
| n |
| n |
| 2 |
| 3 |
| 2 |
| m |
| n |
| n |
| 2m |
| 3 |
| 2 |
| 2 |
又2m+n=2,
∴m=2-
| 2 |
| 2 |
点评:本题考查复数的基本概念的应用,基本不等式的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列函数中,以π为周期的偶函数是( )
| A、y=sin|x| | ||
| B、y=|cosx| | ||
C、y=cos(2x-
| ||
D、y=sin(x+
|
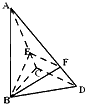 已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且
已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且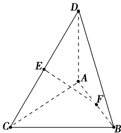 已知DA⊥平面ABC,AC⊥CB,AC=CB=AD=2,E是DC的中点,F是AB的中点.
已知DA⊥平面ABC,AC⊥CB,AC=CB=AD=2,E是DC的中点,F是AB的中点.