题目内容
若m=（x+3）（x+7），n=（x+4）（x+6），则m，n的大小关系为（ ）
| A、m＜n | B、m=n |
| C、m＞n | D、不确定 |
考点：不等式比较大小
专题：不等式的解法及应用
分析：利用整式的乘法和“作差法”即可得出．
解答：
解：n-m=（x+4）（x+6）-（x+3）（x+7）=（x2+10x+24）-（x2+10x+21）=3＞0，
∴n＞m．
故选：A．
∴n＞m．
故选：A．
点评：本题考查了整式的乘法和“作差法”、不等式的性质，属于基础题．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
某校要求每位学生从7门课程中选修4门，其中甲、乙两门课程不能都选，则不同的选课方案有（ ）
| A、35种 | B、16种 |
| C、20种 | D、25种 |
若实数x为10和90的等差中项，则x的值为（ ）
| A、30 | B、40 | C、50 | D、60 |
已知x∈（0，
），则y=x
的最大值为（ ）
| 1 |
| 4 |
| 1-4x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列函数中，以π为周期的偶函数是（ ）
| A、y=sin|x| | ||
| B、y=|cosx| | ||
C、y=cos（2x-
| ||
D、y=sin（x+
|
已知椭圆
+
=1，则以点M（-1，1）为中点的弦所在直线方程为（ ）
| x2 |
| 4 |
| y2 |
| 3 |
| A、3x-4y+7=0 |
| B、3x+4y-1=0 |
| C、4x-3y+7=0 |
| D、4x+3y+1=0 |
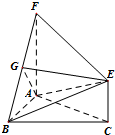如图，三角形ABC和梯形ACEF所在的平面互相垂直，AB⊥BC，AF⊥AC，AF
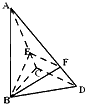已知三棱锥A-BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E、F分别是AC、AD上的动点，且