题目内容
已知集合A既是分式不等式
<1的解集,又是一元二次不等式x2+ax+b>0的解集.
(1)求集合A;
(2)求实数a,b的值.
| 1 |
| x-3 |
(1)求集合A;
(2)求实数a,b的值.
考点:其他不等式的解法,一元二次不等式的解法
专题:不等式的解法及应用
分析:(1)解分式不等式求得A.
(2)根据A利用韦达定理求得实数a,b的值.
(2)根据A利用韦达定理求得实数a,b的值.
解答:
解:(1)
<1⇒
-1<0⇒
<0⇒(4-x)(x-3)<0⇒x<3或x>4,
所以集合A=(-∞,3)∪(4,+∞).
(2)根据集合A为一元二次不等式x2+ax+b>0的解集,则方程x2+ax+b=0的根即为x1=3,x2=4,
由韦达定理知
⇒
.
| 1 |
| x-3 |
| 1 |
| x-3 |
| 4-x |
| x-3 |
所以集合A=(-∞,3)∪(4,+∞).
(2)根据集合A为一元二次不等式x2+ax+b>0的解集,则方程x2+ax+b=0的根即为x1=3,x2=4,
由韦达定理知
|
|
点评:本题主要考查分式不等式、一元二次不等式的解法,韦达定理的应用,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
已知x∈(0,
),则y=x
的最大值为( )
| 1 |
| 4 |
| 1-4x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
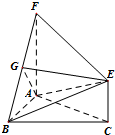 如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF
如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF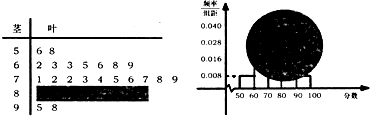 某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如图(阴影部分为损坏数据).据此解答如下问题:
某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如图(阴影部分为损坏数据).据此解答如下问题: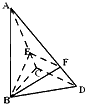 已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且
已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且