题目内容
(本小题满分14分)
已知函数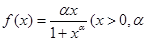 为常数,数列
为常数,数列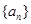 满足:
满足: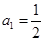 ,
,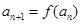 ,
,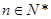 .
.
(1)当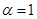 时,求数列
时,求数列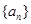 的通项公式;
的通项公式;
(2)在(1)的条件下,证明对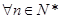 有:
有: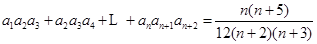 ;
;
(3)若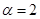 ,且对
,且对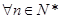 ,有
,有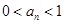 ,证明:
,证明: .
.
已知函数
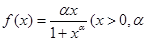 为常数,数列
为常数,数列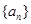 满足:
满足: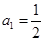 ,
,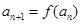 ,
,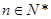 .
.(1)当
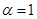 时,求数列
时,求数列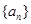 的通项公式;
的通项公式;(2)在(1)的条件下,证明对
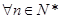 有:
有: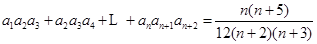 ;
;(3)若
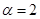 ,且对
,且对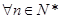 ,有
,有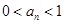 ,证明:
,证明: .
.(1)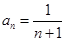 ,
,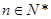
(2)可以用裂项法求和进而证明也可以用数学归纳法证明
(3)可以用基本不等式证明也可以用导数证明,还可以利用数列的单调性证明
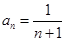 ,
,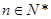
(2)可以用裂项法求和进而证明也可以用数学归纳法证明
(3)可以用基本不等式证明也可以用导数证明,还可以利用数列的单调性证明
试题分析:(1)当
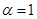 时,
时,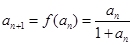 ,
,两边取倒数,得
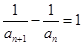 , ……2分
, ……2分故数列
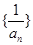 是以
是以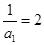 为首项,为公差的等差数列,
为首项,为公差的等差数列,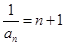 ,
,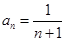 ,
,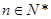 . ……4分
. ……4分(2)证法1:由(1)知
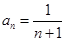 ,故对
,故对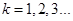
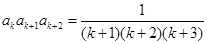
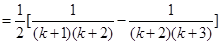 ……6分
……6分所以
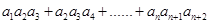
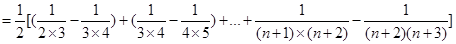
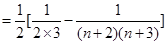
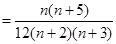 . ……9分
. ……9分[证法2:①当n=1时,等式左边
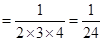 ,等式右边
,等式右边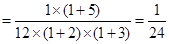 ,左边=右边,等式成立; ……5分
,左边=右边,等式成立; ……5分②假设当
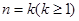 时等式成立,
时等式成立,即
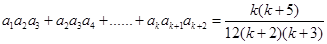 ,
,则当
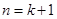 时
时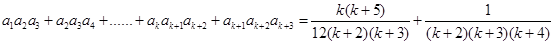
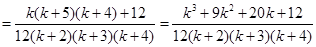
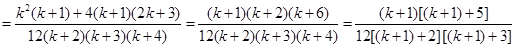
这就是说当
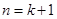 时,等式成立, ……8分
时,等式成立, ……8分综①②知对于
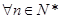 有:
有: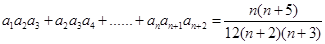 . ……9分】
. ……9分】(3)当
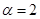 时,
时,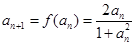
则
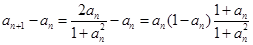 , ……10分
, ……10分∵
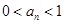 ,
,∴
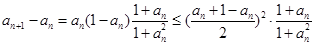 ……11分
……11分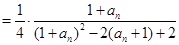
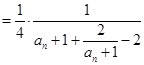
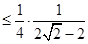
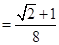 . ……13分
. ……13分∵
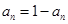 与
与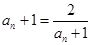 不能同时成立,∴上式“=”不成立,
不能同时成立,∴上式“=”不成立,即对
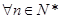 ,
, . ……14分
. ……14分【证法二:当
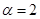 时,
时,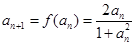 ,
,则
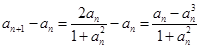 ……10分
……10分又
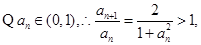
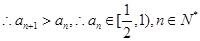 ……11分
……11分令
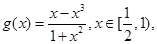 则
则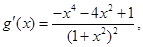 ……12分
……12分当
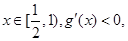 所以函数
所以函数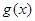 在
在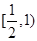 单调递减,故当
单调递减,故当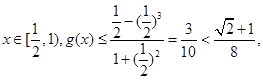 所以命题得证 ……14分】
所以命题得证 ……14分】【证法三:当
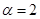 时,
时,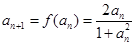 ,
,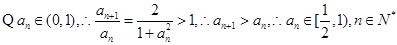 ……11分
……11分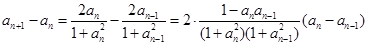
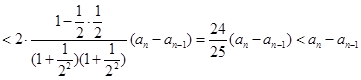
 数列
数列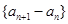 单调递减,
单调递减,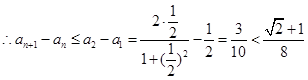 ,
,所以命题得证 ……14分】
点评:本小题比较综合,既考查了数列的通项公式的求解,也考查了数列的前n项的求解,还考查了数列的性质的应用以及基本不等式、导数等的综合应用,难度较大,要求学生具有较高的分析问题、转化问题、解决问题的能力和运算求解能力.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
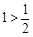 ,
,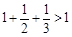 ,
,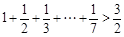 ,
,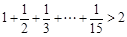 ,
,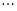 ,你能得到一个怎样的一般不等式?并加以证明.
,你能得到一个怎样的一般不等式?并加以证明.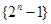 的前
的前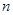 项组成集合
项组成集合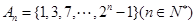 ,从集合
,从集合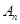 中任取
中任取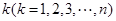 个数,其所有可能的
个数,其所有可能的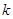 个数的乘积的和为
个数的乘积的和为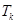 (若只取一个数,规定乘积为此数本身),记
(若只取一个数,规定乘积为此数本身),记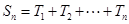 .例如:当
.例如:当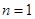 时,
时,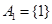 ,
,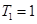 ,
,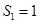 ;当
;当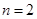 时,
时,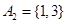 ,
,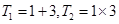 ,
,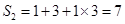 .
.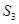 ;
;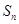 ,并用数学归纳法证明.
,并用数学归纳法证明.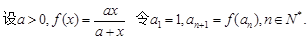
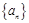 中,
中,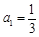 ,且前
,且前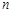 项的算术平均数等于第
项的算术平均数等于第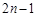 倍(
倍(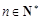 )。
)。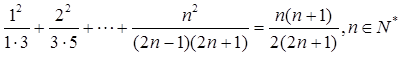
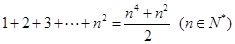 时,则当
时,则当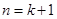 时左端应在
时左端应在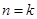 的基础上加上的项是( )
的基础上加上的项是( )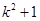
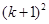
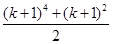
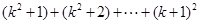
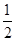 +
+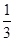 +…+
+…+ <n(n∈N*,n>1)时,在证明过程的第二步从n=k到n=k+1时,左边增加的项数是 ( )
<n(n∈N*,n>1)时,在证明过程的第二步从n=k到n=k+1时,左边增加的项数是 ( )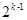
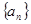 中,数列的前n项和
中,数列的前n项和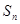 满足
满足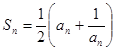
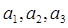 ;(2) 由(1)猜想数列
;(2) 由(1)猜想数列