题目内容
在用数学归纳法证明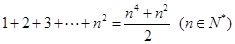 时,则当
时,则当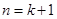 时左端应在
时左端应在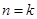 的基础上加上的项是( )
的基础上加上的项是( )
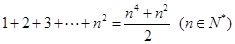 时,则当
时,则当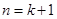 时左端应在
时左端应在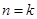 的基础上加上的项是( )
的基础上加上的项是( )A.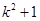 | B.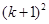 |
C.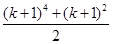 | D.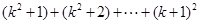 |
D
试题分析:
 时左端为
时左端为 ,
, 时左端为
时左端为 ,观察式子的变化规律可知是连续的正整数相加,因此需增加的项
,观察式子的变化规律可知是连续的正整数相加,因此需增加的项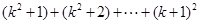
点评:数学归纳法常用来证明与正整数有关的题目,大致步骤:1,证明n取最小的正整数时命题成立,2,假设
 时命题成立,借助假设证明
时命题成立,借助假设证明 时命题成立,由1,2综合得证命题成立
时命题成立,由1,2综合得证命题成立
练习册系列答案
相关题目
题目内容
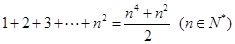 时,则当
时,则当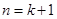 时左端应在
时左端应在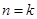 的基础上加上的项是( )
的基础上加上的项是( )A.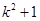 | B.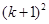 |
C.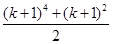 | D.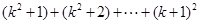 |
 时左端为
时左端为 ,
, 时左端为
时左端为 ,观察式子的变化规律可知是连续的正整数相加,因此需增加的项
,观察式子的变化规律可知是连续的正整数相加,因此需增加的项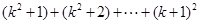
 时命题成立,借助假设证明
时命题成立,借助假设证明 时命题成立,由1,2综合得证命题成立
时命题成立,由1,2综合得证命题成立