题目内容
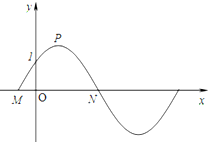 已知如图,函数y=2sin(
已知如图,函数y=2sin(| π |
| 2 |
| π |
| 2 |
(1)求φ的值;
(2)设点P是图象上的最高点,M,N是图象与x轴的交点,求向量
| PM |
| PN |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:(1)由y=2sin(
x+φ)的图象与y轴的交点为(0,1),可得sinφ=
,0≤φ≤
,从而可得φ的值;
(2)依题意,可求得M,N,P的坐标,于是可得向量
与
的坐标,利用向量数量积的坐标运算即可求得向量
与向量
夹角的余弦值
| π |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
(2)依题意,可求得M,N,P的坐标,于是可得向量
| PM |
| PN |
| PM |
| PN |
解答:
解:(1)由题意得2sinφ=1,sinφ=
,0≤φ≤
,
∴φ=
.…..…(6分)
(2)由
x+
=0得:x=-
,
∴M(-
,0),又T=
=4,
∴点P的横坐标xp=(-
)+
T=
,
∴P(
,2),同理可得N(
,0),…(9分)
∴
=(-1,-2),
=(1,-2),…(12分)
设向量
与的
夹角为θ,则cosθ=
=
…(14分)
| 1 |
| 2 |
| π |
| 2 |
∴φ=
| π |
| 6 |
(2)由
| π |
| 2 |
| π |
| 6 |
| 1 |
| 3 |
∴M(-
| 1 |
| 3 |
| 2π | ||
|
∴点P的横坐标xp=(-
| 1 |
| 3 |
| 1 |
| 4 |
| 2 |
| 3 |
∴P(
| 2 |
| 3 |
| 5 |
| 3 |
∴
| PM |
| PN |
设向量
| PM |
| PN |
| ||||
|
|
| 3 |
| 5 |
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,着重考查向量数量积的坐标运算,求得M,N,P的坐标是关键,考查运算能力,属于中档题.

练习册系列答案
相关题目
若关于x的不等式|x-1|+|x-4|<a的解集为空集,则a的取值范围为( )
| A、a≥3 | B、a≤3 |
| C、a≥5 | D、a≤5 |
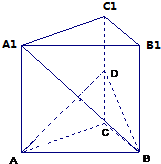 如图,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,AC=BC=2,∠ACB=90°,侧棱AA1=2,D是CC1的中点.
如图,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,AC=BC=2,∠ACB=90°,侧棱AA1=2,D是CC1的中点.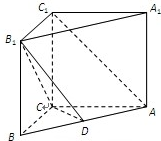 已知直三棱柱ABC-A1B1C1中,AC=BC=AA1=4,AC⊥BC,若D是AB中点.
已知直三棱柱ABC-A1B1C1中,AC=BC=AA1=4,AC⊥BC,若D是AB中点.