题目内容
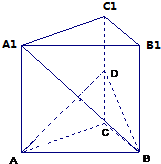 如图,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,AC=BC=2,∠ACB=90°,侧棱AA1=2,D是CC1的中点.
如图,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,AC=BC=2,∠ACB=90°,侧棱AA1=2,D是CC1的中点.(1)求二面角D-AB-C的平面角的正切值;
(2)求A1B与平面BB1C1C所成角的正弦值.
考点:二面角的平面角及求法,直线与平面所成的角
专题:计算题,空间角
分析:(Ⅰ)取AB中点E,连接DE,CE,证明∠DEC即为二面角D-AB-C的平面角,即可求二面角D-AB-C的平面角的正切值;
(2)连接BC1,证明∠A1BC1即为A1B与平面BB1C1C所成角,即可求A1B与平面BB1C1C所成角的正弦值.
(2)连接BC1,证明∠A1BC1即为A1B与平面BB1C1C所成角,即可求A1B与平面BB1C1C所成角的正弦值.
解答:
 解:(Ⅰ)取AB中点E,连接DE,CE
解:(Ⅰ)取AB中点E,连接DE,CE
因为直棱柱,CC1⊥面ABC,所以CC1⊥AB,
又因为△ABC为等腰直角三角形,
所以CE⊥AB,所以AB⊥面DEC,即AB⊥DE,
所以∠DEC即为二面角D-AB-C的平面角
因为CD=1,CE=
,则tan∠DEC=
=
=
(II)连接BC1.
因为直棱柱,所以CC1⊥AC,且AC∥A1C1,所以CC1⊥A1C1.
而由于AC⊥BC,所以A1C1⊥B1C1,
所以A1C1⊥面BB1C1C,
所以∠A1BC1即为A1B与平面BB1C1C所成角.
因为A1C1=2,BC1=2
,所以sin∠A1BC1=
.
 解:(Ⅰ)取AB中点E,连接DE,CE
解:(Ⅰ)取AB中点E,连接DE,CE因为直棱柱,CC1⊥面ABC,所以CC1⊥AB,
又因为△ABC为等腰直角三角形,
所以CE⊥AB,所以AB⊥面DEC,即AB⊥DE,
所以∠DEC即为二面角D-AB-C的平面角
因为CD=1,CE=
| 2 |
| DC |
| CE |
| 1 | ||
|
| ||
| 2 |
(II)连接BC1.
因为直棱柱,所以CC1⊥AC,且AC∥A1C1,所以CC1⊥A1C1.
而由于AC⊥BC,所以A1C1⊥B1C1,
所以A1C1⊥面BB1C1C,
所以∠A1BC1即为A1B与平面BB1C1C所成角.
因为A1C1=2,BC1=2
| 2 |
| ||
| 3 |
点评:本题考查空间角的计算,考查学生的计算能力,正确作出空间角是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知一个线性回归方程为
=1.5x+45,其中x的取值依次为1,7,5,13,19,则
=( )
 |
| y |
. |
| y |
| A、58.5 | B、46.5 |
| C、60 | D、75 |

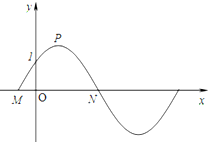 已知如图,函数y=2sin(
已知如图,函数y=2sin(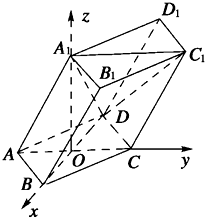 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°.
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°.