题目内容
已知函数f(x)=sin(2ωx+
)(ω>0)直线x=x1,x=x2是y=f(x)图象的任意两条对称轴,且|x1-x2|的最小值为
.
(1)求函数f(x)的单调增区间;
(2)若f(α)=
,α∈[-
,
],求f(α+
)的值;
(3)若关于x的方程f(x+
)+mcosx+3=0在x∈(0,
)有实数解,求实数m的取值.
| π |
| 6 |
| π |
| 2 |
(1)求函数f(x)的单调增区间;
(2)若f(α)=
| 1 |
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
(3)若关于x的方程f(x+
| π |
| 6 |
| π |
| 2 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:(1)由题意可得函数的最小正周期T=2×
=
,解得ω=1,可得f(x)=sin(2x+
).令2kπ-
≤2x+
≤2kπ+
,k∈z,求得x的范围,可得函数的增区间.
(2)由f(α)=sin(2α+
)=
,2α+
∈[-
,
],求得cos(2α+
)的值,再由f(α+
)=sin(2α+
)=cos2α=cos[(2α+
)-
],利用两角差的余弦公式计算求得结果.
(3)由题意可得即2cos2x+mcosx+2=0,在x∈(0,
)有实数解.令cosx=t∈(0,1),则2t2+mt+2=0在(0,1)上有解.令g(t)=2t2+mt+2,利用二次函数的性质求得m的范围.
| π |
| 2 |
| 2π |
| 2ω |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
(2)由f(α)=sin(2α+
| π |
| 6 |
| 1 |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
(3)由题意可得即2cos2x+mcosx+2=0,在x∈(0,
| π |
| 2 |
解答:
解:(1)∵函数f(x)=sin(2ωx+
)(ω>0),直线x=x1、x=x2是y=f(x)图象的两条对称轴,
且|x1-x2|的最小值为
,
∴函数的最小正周期T=2×
=
,解之得ω=1,故f(x)=sin(2x+
).
令2kπ-
≤2x+
≤2kπ+
,k∈z,求得kπ-
≤x≤kπ+
,
故函数的增区间为[kπ-
,kπ+
],k∈z.
(2)∵f(α)=sin(2α+
)=
,α∈[-
,
],∴2α+
∈[-
,
],
∴cos(2α+
)=
,
求得 f(α+
)=sin(2α+
)=cos2α=cos[(2α+
)-
]=cos(2α+
)cos
+sin(2α+
)sin
=
×
+
×
=
.
(3)关于x的方程f(x+
)+mcosx+3=0,即 cos2x+mcosx+3=0,
即2cos2x+mcosx+2=0,在x∈(0,
)有实数解.
令cosx=t∈(0,1),则2t2+mt+2=0在(0,1)上有解.
令g(t)=2t2+mt+2,∵△=m2-16≥0,∴m≥4,或m≤-4.
由于对称轴为t=-
≥1,或 t=-
≤-1,
∵g(0)=2>0,∴由图象可得 g(1)=m+4<0,解得m<-4.

| π |
| 6 |
且|x1-x2|的最小值为
| π |
| 2 |
∴函数的最小正周期T=2×
| π |
| 2 |
| 2π |
| 2ω |
| π |
| 6 |
令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
故函数的增区间为[kπ-
| π |
| 3 |
| π |
| 6 |
(2)∵f(α)=sin(2α+
| π |
| 6 |
| 1 |
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
∴cos(2α+
| π |
| 6 |
2
| ||
| 3 |
求得 f(α+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
=
2
| ||
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
2
| ||
| 6 |
(3)关于x的方程f(x+
| π |
| 6 |
即2cos2x+mcosx+2=0,在x∈(0,
| π |
| 2 |
令cosx=t∈(0,1),则2t2+mt+2=0在(0,1)上有解.
令g(t)=2t2+mt+2,∵△=m2-16≥0,∴m≥4,或m≤-4.
由于对称轴为t=-
| m |
| 4 |
| m |
| 4 |
∵g(0)=2>0,∴由图象可得 g(1)=m+4<0,解得m<-4.

点评:本题主要考查正弦函数的图象和性质,三角恒等变换,二次函数的性质应用,属于中档题.

练习册系列答案
相关题目
从混有5张假钞的20张百元钞票中任意抽取两张2张,将其中一张在验钞机上检验发现是假钞,问这2张都是假钞的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
某曲线y=f(x)在x=5处的切线方程为y=-x+8,则f(5)+f′(5)=( )
| A、6 | B、2 | C、4 | D、-2 |
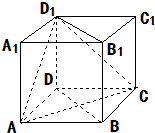 如图,在正方体ABCD-A1B1C1D1中.求证:平面ACD1⊥平面BB1D1D.
如图,在正方体ABCD-A1B1C1D1中.求证:平面ACD1⊥平面BB1D1D.
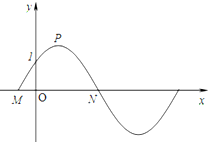 已知如图,函数y=2sin(
已知如图,函数y=2sin(