题目内容
已知集合A={x|x2-3x-10≤0}
(1)若B⊆A,B={x|m+1≤x≤2m-1},求实数m的取值范围;
(2)若A⊆B,B={x|m-6≤x≤2m-1},求实数m的取值范围.
(1)若B⊆A,B={x|m+1≤x≤2m-1},求实数m的取值范围;
(2)若A⊆B,B={x|m-6≤x≤2m-1},求实数m的取值范围.
考点:集合的包含关系判断及应用
专题:集合
分析:(1)先求出A={x|-2≤x≤5},若B⊆A,则:B=∅时,m+1>2m-1,m<2;B≠∅时,则m应满足
,所以解该不等式组,并合并m<2即得m的取值范围;
(2)若A⊆B,则m应满足
,解该不等式组即得m的取值范围.
|
(2)若A⊆B,则m应满足
|
解答:
解:A={x|-2≤x≤5};
(1)∵B⊆A;
∴①若B=∅,则m+1>2m-1,即m<2,此时满足B⊆A;
②若B≠∅,则
;
解得2≤m≤3;
由①②得,m的取值范围是(-∞,3];
(2)若A⊆B,则
;
解得3≤m≤4;
∴m的取值范围是[3,4].
(1)∵B⊆A;
∴①若B=∅,则m+1>2m-1,即m<2,此时满足B⊆A;
②若B≠∅,则
|
解得2≤m≤3;
由①②得,m的取值范围是(-∞,3];
(2)若A⊆B,则
|
解得3≤m≤4;
∴m的取值范围是[3,4].
点评:考查解一元二次不等式,子集、空集的概念,以及描述法表示集合.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
设函数f(x)是(-∞,+∞)上的减函数,又若a∈R,则( )
| A、f (a)>f(2a) |
| B、f (a2)<f(a) |
| C、f (a2+a)<f(a) |
| D、f(a2+1)<f(a) |
已知a=0.5-
,b=(
)-
,c=log2.51.5,则a,b,c的大小关系( )
| 1 |
| 3 |
| 3 |
| 5 |
| 1 |
| 3 |
| A、c<a<b |
| B、c<b<a |
| C、a<b<c |
| D、b<a<c |
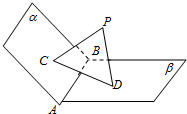 如图,已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足.且PC=PD=CD=1,则二面角α-AB-β的大小是( )
如图,已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足.且PC=PD=CD=1,则二面角α-AB-β的大小是( )| A、120° | B、45° |
| C、60° | D、150° |
已知向量
、
、
是单位向量,且
•
=0,则(
-
)•(
-
)的最大值为( )
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| b |
| c |
A、
| ||
B、2+
| ||
C、
| ||
D、
|