题目内容
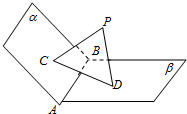 如图,已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足.且PC=PD=CD=1,则二面角α-AB-β的大小是( )
如图,已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足.且PC=PD=CD=1,则二面角α-AB-β的大小是( )| A、120° | B、45° |
| C、60° | D、150° |
考点:二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:过C作CE⊥AB,交AB于E,连接DE,通过已知条件容易说明∠CED便是二面角α-AB-β的平面角,并可说明C,E,D,P四点共面.所以在四边形PCED中,∠PCE=∠PDE=90°,所以∠CED和∠CPD互补,根据已知条件知∠CPD=60°,所以∠CED=120°.
解答:
解:如图,过C作CE⊥AB,交AB于E,并连接DE;
 ∵PC⊥α,PD⊥β,AB?α,AB?β;
∵PC⊥α,PD⊥β,AB?α,AB?β;
∴PC⊥AB,PD⊥AB,即AB⊥PC,AB⊥PD,PC∩PD=P;
∴AB⊥平面PCD,∴AB⊥CD,又AB⊥CE;
∴AB⊥平面CDE,AB⊥DE;
∴∠CED是二面角α-AB-β的平面角;
由前面知,平面PCD和平面CDE是一个平面;
∴在四边形PCED中,∠PCE=∠PDE=90°,又根据已知条件∠CPD=60°;
∴∠CED=120°;
即二面角α-AB-β的大小是120°.
故选A.
 ∵PC⊥α,PD⊥β,AB?α,AB?β;
∵PC⊥α,PD⊥β,AB?α,AB?β;∴PC⊥AB,PD⊥AB,即AB⊥PC,AB⊥PD,PC∩PD=P;
∴AB⊥平面PCD,∴AB⊥CD,又AB⊥CE;
∴AB⊥平面CDE,AB⊥DE;
∴∠CED是二面角α-AB-β的平面角;
由前面知,平面PCD和平面CDE是一个平面;
∴在四边形PCED中,∠PCE=∠PDE=90°,又根据已知条件∠CPD=60°;
∴∠CED=120°;
即二面角α-AB-β的大小是120°.
故选A.
点评:考查线面垂直的性质,线面垂直的判定定理,以及二面角及二面角的平面角的定义,及二面角的平面角的找法.

练习册系列答案
相关题目
设集合A={0,1,2,3},集合B={2,3,4},则A∩B=( )
| A、{2,3} |
| B、{0,1} |
| C、{0,1,4} |
| D、{0,1,2,3,4} |
若3x=9,log2
=y,则x+2y等于( )
| 8 |
| 3 |
| A、6 |
| B、8-2log23 |
| C、4 |
| D、log48 |
 如图所示,已知三棱柱ABC-A′B′C′,侧面B′BCC′的面积是S,点A′到侧面B′BCC′的距离是a,求三棱柱ABC-A′B′C′的体积.
如图所示,已知三棱柱ABC-A′B′C′,侧面B′BCC′的面积是S,点A′到侧面B′BCC′的距离是a,求三棱柱ABC-A′B′C′的体积.