题目内容
2.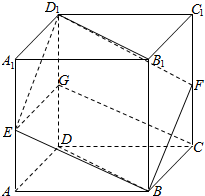 如图,已知E、F、G分别是棱长为2的正方体ABCD-A1B1C1D1的棱AA1、CC1、DD1的中点.
如图,已知E、F、G分别是棱长为2的正方体ABCD-A1B1C1D1的棱AA1、CC1、DD1的中点.(1)判断多面体EGD1BCF是否是棱柱,并求它的体积;
(2)求证:平面EBFD1⊥平面BB1D1D.
分析 (1)充分利用正方体的对称性,可通过三角形全等证明多面体EGD1BCF是棱柱;
(2)由E、F是正方体对棱的中点,可得四边形EBFD1为菱形,从而得到线线垂直,问题将迎刃而解.
解答 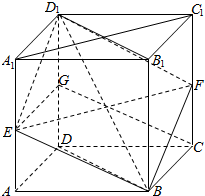 (1)解:由题意△D1EG≌△FBC,平面D1EG∥平面FBC,
(1)解:由题意△D1EG≌△FBC,平面D1EG∥平面FBC,
∴多面体EGD1BCF是棱柱;
多面体EGD1BCF的体积=$\frac{1}{2}×2×1×2$=2;
(2)证明:在正方体ABCD-A1B1C1D1中,∵四边形EBFD1是平行四边形.AE=A1E,FC=FC1,
∴Rt△EAB≌Rt△FCB,∴BE=BF,故四边形EBFD1为菱形.
连结EF、BD1、A1C1.
∵四边形EBFD1为菱形,∴EF⊥BD1,
在正方体ABCD-A1B1C1D1中,有B1D1⊥A1C1,B1D1⊥A1A,∴B1D1⊥平面A1ACC1.
又EF?平面A1ACC1,∴EF⊥B1D1.
又B1D1∩BD1=D1,∴EF⊥平面BB1D1D.
又EF?平面EBFD1,故平面EBFD1⊥平面BB1D1D.
点评 证明面面垂直的关键是证明线面垂直,而线面垂直又是通过线线垂直实现的,充分利用正方体的对称性,通过证明四边形EBFD1是菱形证明线线垂直是本题证明的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
14.下列各组向量中不平行的是( )
| A. | $\overrightarrow{a}$=(1,2,-2),$\overrightarrow{b}$=(-2,-4,4) | B. | $\overrightarrow{c}$=(1,0,0),$\overrightarrow{d}$=(-3,0,0) | ||
| C. | $\overrightarrow{e}$=(2,3,0),$\overrightarrow{f}$=(0,0,0) | D. | $\overrightarrow{g}$=(-2,3,5)$\overrightarrow{h}$=(16,-24,40) |
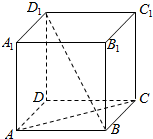 如图,在棱长为2的正方体ABCD-A1B1C1D1中,过AC且与直线D1B平行的截面交D1D于点M,则△MAC的面积为=$\sqrt{6}$.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,过AC且与直线D1B平行的截面交D1D于点M,则△MAC的面积为=$\sqrt{6}$.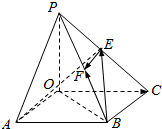 如图,四棱锥P-OABC的底面为一矩形,PO⊥平面OABC.设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$,$\overrightarrow{OP}$=$\overrightarrow{c}$,E,F分别是PC和PB的中点,用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{BF}$、$\overrightarrow{BE}$、$\overrightarrow{AE}$、$\overrightarrow{EF}$.
如图,四棱锥P-OABC的底面为一矩形,PO⊥平面OABC.设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$,$\overrightarrow{OP}$=$\overrightarrow{c}$,E,F分别是PC和PB的中点,用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{BF}$、$\overrightarrow{BE}$、$\overrightarrow{AE}$、$\overrightarrow{EF}$.