题目内容
11.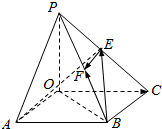 如图,四棱锥P-OABC的底面为一矩形,PO⊥平面OABC.设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$,$\overrightarrow{OP}$=$\overrightarrow{c}$,E,F分别是PC和PB的中点,用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{BF}$、$\overrightarrow{BE}$、$\overrightarrow{AE}$、$\overrightarrow{EF}$.
如图,四棱锥P-OABC的底面为一矩形,PO⊥平面OABC.设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$,$\overrightarrow{OP}$=$\overrightarrow{c}$,E,F分别是PC和PB的中点,用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{BF}$、$\overrightarrow{BE}$、$\overrightarrow{AE}$、$\overrightarrow{EF}$.
分析 根据空间向量的线性运算的几何意义,用向量$\overrightarrow{OA}$、$\overrightarrow{OC}$与$\overrightarrow{OP}$分别表示$\overrightarrow{BF}$、$\overrightarrow{BE}$、$\overrightarrow{AE}$和$\overrightarrow{EF}$.
解答  解:如图所示,
解:如图所示,
四棱锥P-OABC中,PO⊥平面OABC,
设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$,$\overrightarrow{OP}$=$\overrightarrow{c}$,E,F分别是PC和PB的中点,
所以$\overrightarrow{BF}$=$\frac{1}{2}$$\overrightarrow{BP}$=$\frac{1}{2}$($\overrightarrow{OP}$-$\overrightarrow{OB}$)=$\frac{1}{2}$$\overrightarrow{OP}$-$\frac{1}{2}$($\overrightarrow{OA}$+$\overrightarrow{OC}$)=$\frac{1}{2}$$\overrightarrow{c}$-$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$,
$\overrightarrow{BE}$=$\overrightarrow{CE}$-$\overrightarrow{CB}$=$\frac{1}{2}$$\overrightarrow{CP}$-$\overrightarrow{OA}$=$\frac{1}{2}$($\overrightarrow{OP}$-$\overrightarrow{OC}$)-$\overrightarrow{OA}$=$\frac{1}{2}$$\overrightarrow{c}$-$\frac{1}{2}$$\overrightarrow{b}$-$\overrightarrow{a}$,
$\overrightarrow{AE}$=$\overrightarrow{OE}$-$\overrightarrow{OA}$=$\frac{1}{2}$($\overrightarrow{OP}$+$\overrightarrow{OC}$)-$\overrightarrow{OA}$=$\frac{1}{2}$$\overrightarrow{c}$+$\frac{1}{2}$$\overrightarrow{b}$-$\overrightarrow{a}$,
$\overrightarrow{EF}$=$\frac{1}{2}$$\overrightarrow{CB}$=$\frac{1}{2}$$\overrightarrow{OA}$=$\frac{1}{2}$$\overrightarrow{a}$.
点评 本题考查了空间向量的线性运算与线性表示的应用问题,也考查了数形结合的解题方法,是基础题目.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案| A. | ($\frac{1}{2}$,2) | B. | (-∞,$\frac{1}{2}$)∪(2,+∞) | C. | ($\frac{1}{2}$,1)∪(2,+∞) | D. | (0,2) |
| A. | 10 | B. | 20 | C. | 16 | D. | 12 |
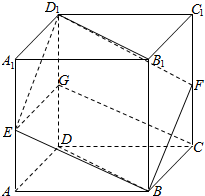 如图,已知E、F、G分别是棱长为2的正方体ABCD-A1B1C1D1的棱AA1、CC1、DD1的中点.
如图,已知E、F、G分别是棱长为2的正方体ABCD-A1B1C1D1的棱AA1、CC1、DD1的中点.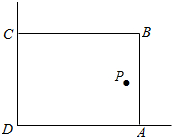 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两墙足够长),用16m长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),在P处有一棵树与墙CD、AD的距离分别是a(0<a<12)m和4m,现需要将这棵树围在花园内(含边界,不考虑树的粗细).设矩形ABCD的面积是ym2,长DA为xm.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两墙足够长),用16m长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),在P处有一棵树与墙CD、AD的距离分别是a(0<a<12)m和4m,现需要将这棵树围在花园内(含边界,不考虑树的粗细).设矩形ABCD的面积是ym2,长DA为xm.