题目内容
4.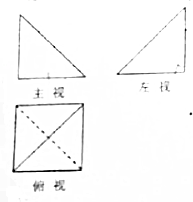 已知一个三棱锥的三视图如图所示,主视图和左视图都是腰长为1的等腰直角三角形,那么,这个三棱锥的表面积为$\frac{1+2\sqrt{2}+\sqrt{3}}{2}$.
已知一个三棱锥的三视图如图所示,主视图和左视图都是腰长为1的等腰直角三角形,那么,这个三棱锥的表面积为$\frac{1+2\sqrt{2}+\sqrt{3}}{2}$.
分析 如图所示,该三棱锥为P-ABC,满足PD⊥底面BAC,D为点P在底面ABC的射影,四边形ABCD是边长为1的正方形,PD=1,即可得出.
解答 解:如图所示,该三棱锥为P-ABC,满足PD⊥底面BAC,D为点P在底面ABC的射影,四边形ABCD是边长为1的正方形,PD=1,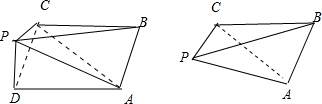
这个三棱锥的表面积S=$\frac{1}{2}×\sqrt{2}×1$+$\frac{1}{2}×1×1$+$\frac{1}{2}×\sqrt{2}×1$+$\frac{1}{2}×\sqrt{2}×$$\sqrt{{1}^{2}+(\frac{\sqrt{2}}{2})^{2}}$=$\frac{1+2\sqrt{2}+\sqrt{3}}{2}$.
故答案为:$\frac{1+2\sqrt{2}+\sqrt{3}}{2}$.
点评 本题考查了三棱锥的三视图、正方形的性质、三角形的面积计算公式,考查了空间想象能力、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x(x>0)}\\{f(x+1)-f(x+2)(x≤0)}\end{array}\right.$,则f(-2016)=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
16.在(1+x)+(1+x)2+(1+x)3+…+(1+x)9的展开式中,x2的系数等于( )
| A. | 280 | B. | 300 | C. | 210 | D. | 120 |
5.复数z=$\frac{2+i}{i}$的共轭复数是( )
| A. | 2+i | B. | 2-i | C. | 1+2i | D. | 1-2i |