题目内容
14.对数列{an},规定{△an}为数列{an}的一阶差分数列,其中△an=an+1-an(n∈N*);一般地,规定{△kan}为数列{an}的k阶差分数列,其中△kan=△k-1an+1-△k-1an(n,k∈N*,k≥2).已知数列{an}的通项公式an=n2+n①△an=2n+2;
②数列{△3an}既是等差数列,又是等比数列;
③数列{△an}的前n项之和为an=n2+n;
④{△2an}的前2015项之和为4030.
则以下结论正确的命题个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据△an=an+1-an 计算可得①正确.根据△2an=2(n+1)+2-(2n+2)=2,得{△2an}是首项为2,公差为0的等差数列,故对数列{△3an},△3an=2-2=0,故②不正确.
计算数列{△an}的前n项之和的值,可得③不正确. 根据{△2an}是首项为2,公差为0的等差数列,求得{△2an}的前2015项之和的值,可得④正确.
解答 解:由于△an=an+1-an(n∈N*),{△kan}为数列{an}的k阶差分数列,△kan=△k-1an+1-△k-1an(n,k∈N*,k≥2).an=n2+n
故△an=an+1-an =(n+1)2+(n+1)-[n2+n]=2n+2,故①正确.
由于△2an=2(n+1)+2-(2n+2)=2,∴{△2an}是首项为2,公差为0的等差数列,故对数列{△3an},△3an=2-2=0,故数列{△3an}是等差数列,但不是等比数列,故②不正确.
数列{△an}的前n项之和为△a1+△a2+…+△an=a2-a1+a3-a2+…+an+1-an=an+1-a1=(n+1)2+(n+1)-[1+1]=n2+3n,故③不正确.
由于△2an=2(n+1)+2-(2n+2)=2,∴{△2an}是首项为2,公差为0的等差数列,{△2an}的前2015项之和为 2×2015=4030,故④正确.
故选:C.
点评 本小题以新定义为载体主要考查等差数列、等比数列的定义的基础知识,考查观察、猜想并进行证明的数学思想方法,还考查了把新的定义转化为利用所学知识进行求解的能力.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
5.函数f(x)=$\left\{\begin{array}{l}{{2}^{-x}}&{(x<1)}\\{lo{g}_{81}x}&{(x≥1)}\end{array}\right.$,则满足f(x)=$\frac{1}{4}$的x的值是( )
| A. | 2 | B. | -2 | C. | 3 | D. | $\frac{1}{3}$ |
2.下列判断不正确的是( )
| A. | 若A,B,C三点共线,则$\overrightarrow{AB}$∥$\overrightarrow{BC}$ | B. | 若$\overrightarrow{AB}$∥$\overrightarrow{BC}$,则A,B,C三点共线 | ||
| C. | 若AB∥CD,则$\overrightarrow{AB}$,$\overrightarrow{CD}$共线 | D. | 若$\vec a$∥$\vec b$,$\vec b$∥$\vec c$,则$\vec a$∥$\vec c$ |
9.已知函数f(x)(x∈R)满足:①?x∈R,有f(x)f(y)=f(x+y)+f(x-y)成立;②?x0∈R,使f(x0)≠0,则下列结论中错误的是( )
| A. | f(0)=2 | B. | 函数f(x)是偶函数 | C. | 函数f(x)是奇函数 | D. | [f(x)+1][f(x)-1]=f(2x)+1 |
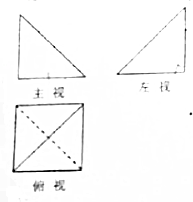 已知一个三棱锥的三视图如图所示,主视图和左视图都是腰长为1的等腰直角三角形,那么,这个三棱锥的表面积为$\frac{1+2\sqrt{2}+\sqrt{3}}{2}$.
已知一个三棱锥的三视图如图所示,主视图和左视图都是腰长为1的等腰直角三角形,那么,这个三棱锥的表面积为$\frac{1+2\sqrt{2}+\sqrt{3}}{2}$.