题目内容
5.复数z=$\frac{2+i}{i}$的共轭复数是( )| A. | 2+i | B. | 2-i | C. | 1+2i | D. | 1-2i |
分析 直接由复数代数形式的乘除运算化简复数z,则复数z=$\frac{2+i}{i}$的共轭复数可求.
解答 解:z=$\frac{2+i}{i}$=$\frac{-i(2+i)}{-{i}^{2}}=1-2i$,
则复数z=$\frac{2+i}{i}$的共轭复数是:1+2i.
故选:C.
点评 本题考查了复数代数形式的乘除运算,考查了共轭复数的求法,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.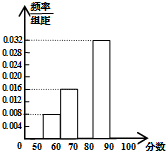 为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
(Ⅰ)补全频率分布直方图;
(Ⅱ)根据频率分布直方图计算学生成绩的平均值.
 为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:(Ⅰ)补全频率分布直方图;
| 分组 | 频数 | 频率 |
| [50,60) | 4 | 0.08 |
| [60,70) | 8 | 0.16 |
| [70,80) | 10 | 0.20 |
| [80,90) | 16 | 0.32 |
| [90,100] | 12 | 0.24 |
| 合计 | 50 | 1 |
17.圆(x+2)2+(y-3)2=5的圆心坐标、半径分别是( )
| A. | (2,-3)、5 | B. | (-2,3)、5 | C. | (-2,3)、$\sqrt{5}$ | D. | ( 3,-2)、$\sqrt{5}$ |
14.定义在R上的偶函数f(x)满足f(x+1)=$\frac{1}{f(x)}$,且f(x)在[-3,-2]上是减函数,若α,β是锐角三角形的两个内角,则( )
| A. | f(sinα)>f(sinβ) | B. | f(cosα)>f(cosβ) | C. | f(sinα)>f(cosβ) | D. | f(sinα)<f(cosβ) |
15.已知$\frac{sinα-2cosα}{3sinα+5cosα}$=5,那么tanα的值为( )
| A. | -2 | B. | 2 | C. | -$\frac{27}{14}$ | D. | -$\frac{23}{16}$ |
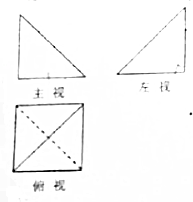 已知一个三棱锥的三视图如图所示,主视图和左视图都是腰长为1的等腰直角三角形,那么,这个三棱锥的表面积为$\frac{1+2\sqrt{2}+\sqrt{3}}{2}$.
已知一个三棱锥的三视图如图所示,主视图和左视图都是腰长为1的等腰直角三角形,那么,这个三棱锥的表面积为$\frac{1+2\sqrt{2}+\sqrt{3}}{2}$.