题目内容
12.以A(1,3)和B(3,5)为直径两端点的圆的标准方程为(x-2)2+(y-4)2=2.分析 求出圆心与半径,即可写出圆的方程.
解答 解:∵A(1,3),B(3,5),
∴|AB|=$\sqrt{{(3-1)}^{2}{+(5-3)}^{2}}$=2$\sqrt{2}$,
且AB的中点C为x=$\frac{1+3}{2}$=2,y=$\frac{3+5}{2}$=4,
即圆心C(2,4),半径r=$\sqrt{2}$;
∴以A和B为直径两端点的圆的标准方程(x-2)2+(y-4)2=2.
故答案为:(x-2)2+(y-4)2=2.
点评 本题考查了求圆的方程的应用问题,是基础题目.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
2.下列判断不正确的是( )
| A. | 若A,B,C三点共线,则$\overrightarrow{AB}$∥$\overrightarrow{BC}$ | B. | 若$\overrightarrow{AB}$∥$\overrightarrow{BC}$,则A,B,C三点共线 | ||
| C. | 若AB∥CD,则$\overrightarrow{AB}$,$\overrightarrow{CD}$共线 | D. | 若$\vec a$∥$\vec b$,$\vec b$∥$\vec c$,则$\vec a$∥$\vec c$ |
17.(x-y)(x+y)8的展开式中x2y7的系数是( )
| A. | -20 | B. | 20 | C. | -22 | D. | 22 |
14.定义在R上的偶函数f(x)满足f(x+1)=$\frac{1}{f(x)}$,且f(x)在[-3,-2]上是减函数,若α,β是锐角三角形的两个内角,则( )
| A. | f(sinα)>f(sinβ) | B. | f(cosα)>f(cosβ) | C. | f(sinα)>f(cosβ) | D. | f(sinα)<f(cosβ) |
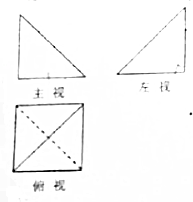 已知一个三棱锥的三视图如图所示,主视图和左视图都是腰长为1的等腰直角三角形,那么,这个三棱锥的表面积为$\frac{1+2\sqrt{2}+\sqrt{3}}{2}$.
已知一个三棱锥的三视图如图所示,主视图和左视图都是腰长为1的等腰直角三角形,那么,这个三棱锥的表面积为$\frac{1+2\sqrt{2}+\sqrt{3}}{2}$.