题目内容
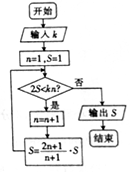
15. 斐波拉契数列0,1,1,2,3,5,8…是数学史上一个著名的数列,定义如下:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N).某同学设计了一个求解斐波拉契数列前15项和的程序框图,那么在空白矩形和判断框内应分别填入的词句是( )
斐波拉契数列0,1,1,2,3,5,8…是数学史上一个著名的数列,定义如下:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N).某同学设计了一个求解斐波拉契数列前15项和的程序框图,那么在空白矩形和判断框内应分别填入的词句是( )| A. | c=a,i≤14 | B. | b=c,i≤14 | C. | c=a,i≤15 | D. | b=c,i≤15 |
分析 模拟程序的运行,可得在每一次循环中,计算出S的值后,变量b的值变为下一个连续三项的第一项a,即a=b,变量c的值为下一个连续三项的第二项b,即b=c从而判断空白矩形框内应为:b=c,由于程序进行循环体前第一次计算S的值时已计算出数列的前两项,只需要循环12次就完成,可求判断框中应填入i≤14.
解答 解:依题意知,程序框图中变量S为累加变量,
变量a,b,c(其中c=a+b)为数列连续三项,
在每一次循环中,计算出S的值后,变量b的值变为下一个连续三项的第一项a,即a=b,
变量c的值为下一个连续三项的第二项b,即b=c,
所以矩形框应填入b=c,
又程序进行循环体前第一次计算S的值时已计算出数列的前两项,
因此只需要循环12次就完成,
所以判断框中应填入i≤14.
故选:B.
点评 本题考查的知识点是程序框图解决实际问题,循环结构有两种形式:当型循环结构和直到型循环结构,当型循环是先判断后循环,直到型循环是先循环后判断.算法和程序框图是新课标新增的内容,在近两年的新课标地区高考都考查到了,这启示我们要给予高度重视,属于基础题.

练习册系列答案
相关题目
7.2${\;}^{\frac{1}{2}+lo{g}_{2}9}$的值是( )
| A. | 12$\sqrt{2}$ | B. | 9+$\sqrt{2}$ | C. | 9$\sqrt{2}$ | D. | 8+$\sqrt{2}$ |
4.函数f(x)=x2-4x+3的最小值是( )
| A. | 3 | B. | 0 | C. | -1 | D. | -2 |
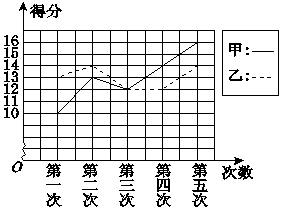 甲、乙二人参加某体育项目训练,近期的五次测试成绩得分情况如图所示.
甲、乙二人参加某体育项目训练,近期的五次测试成绩得分情况如图所示.