题目内容
5.在△ABC中,点B(4,4),角A的内角平分线所在直线的方程为y=0,BC边上的高所在直线的方程为x-2y+2=0(Ⅰ) 求点C的坐标;
(Ⅱ) 求△ABC的面积.
分析 (I)利用相互垂直的直线斜率之间的关系、直线交点与方程组的关系即可得出.
(II)l利用两点之间的距离公式、点到直线的距离公式、三角形面积计算公式即可得出.
解答 解:(Ⅰ)由题意知BC的斜率为-2,又点B(4,4),∴直线BC的方程为y-4=-2(x-4),即2x+y-12=0.
解方程组$\left\{\begin{array}{l}{y=0}\\{x-2y+2=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x=-2}\\{y=0}\end{array}\right.$,∴点A的坐标为(-2,0).
又∠A的内角平分线所在直线的方程为y=0,∴点B(4,4)关于直线y=0的对称点B'(4,-4)在直线AC上,
∴直线AC的方程为$y=-\frac{2}{3}({x+2})$,即2x+3y+4=0.
解方程组$\left\{\begin{array}{l}{2x+y-12=0}\\{2x+3y+4=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x=10}\\{y=-8}\end{array}\right.$,∴点C的坐标为(10,-8).
(Ⅱ)∵$|{BC}|=\sqrt{{{({10-4})}^2}+{{({-8-4})}^2}}=6\sqrt{5}$,
又直线BC的方程是2x+y-12=0,∴点A到直线BC的距离是$d=\frac{{|{2×({-2})-0-12}|}}{{\sqrt{{2^2}+{1^2}}}}=\frac{16}{{\sqrt{5}}}$,∴△ABC的面积是$S=\frac{1}{2}×|{BC}|×d=\frac{1}{2}×6\sqrt{5}×\frac{16}{{\sqrt{5}}}=48$.
点评 本题考查了相互垂直的直线斜率之间的关系、直线交点与方程组的关系、两点之间的距离公式、点到直线的距离公式、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

 高中必刷题系列答案
高中必刷题系列答案 斐波拉契数列0,1,1,2,3,5,8…是数学史上一个著名的数列,定义如下:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N).某同学设计了一个求解斐波拉契数列前15项和的程序框图,那么在空白矩形和判断框内应分别填入的词句是( )
斐波拉契数列0,1,1,2,3,5,8…是数学史上一个著名的数列,定义如下:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N).某同学设计了一个求解斐波拉契数列前15项和的程序框图,那么在空白矩形和判断框内应分别填入的词句是( )| A. | c=a,i≤14 | B. | b=c,i≤14 | C. | c=a,i≤15 | D. | b=c,i≤15 |
| 支持 | 保留 | 不支持 | |
| 30岁以下 | 900 | 120 | 280 |
| 30岁以上(含30岁) | 300 | 260 | 140 |
(Ⅱ)在持“不支持”态度的人中,用分层抽样的方法抽取6人做进一步的调研,将此6人看作一个总体,在这6人中任意选取2人,求至少有1人在30岁以上的概率.
| A. | 0.6 | B. | 0.4 | C. | 0.3 | D. | 0.2 |
| A. | $\frac{63}{32}$ | B. | $\frac{31}{16}$ | C. | $\frac{123}{64}$ | D. | $\frac{127}{128}$ |
 已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π),其部分图象如图,则函数f(x)的解析式为( )
已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π),其部分图象如图,则函数f(x)的解析式为( )| A. | $f(x)=2sin({\frac{1}{2}x+\frac{π}{4}})$ | B. | $f(x)=2sin({\frac{1}{2}x+\frac{3π}{4}})$ | C. | $f(x)=2sin({\frac{1}{4}x+\frac{3π}{4}})$ | D. | $f(x)=2sin({2x+\frac{π}{4}})$ |
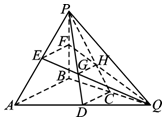 已知:在三棱锥P-ABQ 中,D,C,E,F分别是AQ,BQ,AP,BP的中点,PD与EQ交于点G,PC与FQ交于点H,连接GH,则多面体ADGE-BCHF的体积与三棱锥P-ABQ体积之比是$\frac{11}{18}$.
已知:在三棱锥P-ABQ 中,D,C,E,F分别是AQ,BQ,AP,BP的中点,PD与EQ交于点G,PC与FQ交于点H,连接GH,则多面体ADGE-BCHF的体积与三棱锥P-ABQ体积之比是$\frac{11}{18}$.