题目内容
5.若($\sqrt{x}$-$\frac{2}{x}$)n的二项展开式中的第五项是常数,则自然数n的值为12.分析 利用二项展开式的通项公式,r=4时x的指数为0,列方程求出n的值.
解答 解:($\sqrt{x}$-$\frac{2}{x}$)n的二项展开式中,通项公式为
Tr+1=${C}_{n}^{r}$•${(\sqrt{x})}^{n-r}$•${(-\frac{2}{x})}^{r}$=(-2)r•${C}_{n}^{r}$•${x}^{\frac{n-3r}{2}}$,
当r=4时,$\frac{n-3×4}{2}$=0,解得n=12;
所以自然数n的值为12.
故答案为:12.
点评 本题考查了二项展开式的通项公式应用问题,是基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
16. 进位制是人们为了计数和运算方便而约定的记数系统,在日常生活中,我们最熟悉、最常用的是十进制.如图是实现将某进制数a化为十进制数b的程序框图,若输入的k=2,a=110,n=3,则输出的b=( )
进位制是人们为了计数和运算方便而约定的记数系统,在日常生活中,我们最熟悉、最常用的是十进制.如图是实现将某进制数a化为十进制数b的程序框图,若输入的k=2,a=110,n=3,则输出的b=( )
 进位制是人们为了计数和运算方便而约定的记数系统,在日常生活中,我们最熟悉、最常用的是十进制.如图是实现将某进制数a化为十进制数b的程序框图,若输入的k=2,a=110,n=3,则输出的b=( )
进位制是人们为了计数和运算方便而约定的记数系统,在日常生活中,我们最熟悉、最常用的是十进制.如图是实现将某进制数a化为十进制数b的程序框图,若输入的k=2,a=110,n=3,则输出的b=( )| A. | 14 | B. | 12 | C. | 6 | D. | 3 |
10.设a>0,b>0,若log4($\frac{1}{a}$+$\frac{1}{b}$)=log2$\sqrt{\frac{1}{ab}}$,则$\frac{1}{a}$+$\frac{1}{b}$的最小值为( )
| A. | 8 | B. | 4 | C. | 1 | D. | $\frac{1}{4}$ |
14.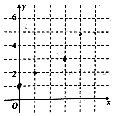 已知实数x、y的取值如表所示
已知实数x、y的取值如表所示
(1)请根据表数据在下面网格纸中绘制散点图;
(2)请根据表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$.
 已知实数x、y的取值如表所示
已知实数x、y的取值如表所示| x | 0 | 1 | 3 | 4 |
| y | 1 | 2 | 3 | 4.4 |
(2)请根据表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$.
15. 斐波拉契数列0,1,1,2,3,5,8…是数学史上一个著名的数列,定义如下:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N).某同学设计了一个求解斐波拉契数列前15项和的程序框图,那么在空白矩形和判断框内应分别填入的词句是( )
斐波拉契数列0,1,1,2,3,5,8…是数学史上一个著名的数列,定义如下:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N).某同学设计了一个求解斐波拉契数列前15项和的程序框图,那么在空白矩形和判断框内应分别填入的词句是( )
 斐波拉契数列0,1,1,2,3,5,8…是数学史上一个著名的数列,定义如下:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N).某同学设计了一个求解斐波拉契数列前15项和的程序框图,那么在空白矩形和判断框内应分别填入的词句是( )
斐波拉契数列0,1,1,2,3,5,8…是数学史上一个著名的数列,定义如下:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N).某同学设计了一个求解斐波拉契数列前15项和的程序框图,那么在空白矩形和判断框内应分别填入的词句是( )| A. | c=a,i≤14 | B. | b=c,i≤14 | C. | c=a,i≤15 | D. | b=c,i≤15 |
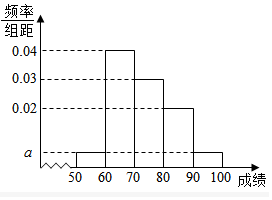 某小学1000名学生期中考试数学成绩的频率分布直方图如图所示.其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].根据统计学的知识估计成绩在[80,90)内的人数约为200.
某小学1000名学生期中考试数学成绩的频率分布直方图如图所示.其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].根据统计学的知识估计成绩在[80,90)内的人数约为200.