题目内容
10.设二项式${({x-\frac{1}{{\sqrt{x}}}})^6}$展开式中的常数项为a,则$\int_0^{\frac{π}{2}}{cos\frac{ax}{5}dx}$的值为-$\frac{1}{3}$.分析 利用二项式定理的通项公式可得a,再利用微积分基本定理即可得出.
解答 解:二项式${({x-\frac{1}{{\sqrt{x}}}})^6}$展开式中的通项公式:Tr+1=${∁}_{6}^{r}$${x}^{6-r}(-\frac{1}{\sqrt{x}})^{r}$=(-1)r${∁}_{6}^{r}$${x}^{6-\frac{3r}{2}}$.
令6-$\frac{3r}{2}$=0,解得r=4.
∴常数项a=${∁}_{6}^{4}$=15,
则$\int_0^{\frac{π}{2}}{cos\frac{ax}{5}dx}$=${∫}_{0}^{\frac{π}{2}}$cos3xdx=$\frac{1}{3}sin3x{|}_{0}^{\frac{π}{2}}$=-$\frac{1}{3}$.
故答案为:-$\frac{1}{3}$.
点评 本题考查了二项式定理的通项公式、微积分基本定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
18. 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数.空气质量分分级与AQI大小关系如表所示:
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数.空气质量分分级与AQI大小关系如表所示:
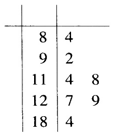
某环保人士从2016年11月甲地的AQI记录数据轴,随机抽取了7天的AQI数据,用茎叶图记录如下:
(Ⅰ)若甲地每年同期的空气质量状况变化不大,请根据统计数据估计2017年11月甲地空气质量为良的天数(结果精确到天);
(Ⅱ)从甲地的这7个数据中任意抽取2个,求AQI均超过100的概率.
 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数.空气质量分分级与AQI大小关系如表所示:
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数.空气质量分分级与AQI大小关系如表所示:| AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | 300以上 |
| 空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
(Ⅰ)若甲地每年同期的空气质量状况变化不大,请根据统计数据估计2017年11月甲地空气质量为良的天数(结果精确到天);
(Ⅱ)从甲地的这7个数据中任意抽取2个,求AQI均超过100的概率.
15. 斐波拉契数列0,1,1,2,3,5,8…是数学史上一个著名的数列,定义如下:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N).某同学设计了一个求解斐波拉契数列前15项和的程序框图,那么在空白矩形和判断框内应分别填入的词句是( )
斐波拉契数列0,1,1,2,3,5,8…是数学史上一个著名的数列,定义如下:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N).某同学设计了一个求解斐波拉契数列前15项和的程序框图,那么在空白矩形和判断框内应分别填入的词句是( )
 斐波拉契数列0,1,1,2,3,5,8…是数学史上一个著名的数列,定义如下:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N).某同学设计了一个求解斐波拉契数列前15项和的程序框图,那么在空白矩形和判断框内应分别填入的词句是( )
斐波拉契数列0,1,1,2,3,5,8…是数学史上一个著名的数列,定义如下:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N).某同学设计了一个求解斐波拉契数列前15项和的程序框图,那么在空白矩形和判断框内应分别填入的词句是( )| A. | c=a,i≤14 | B. | b=c,i≤14 | C. | c=a,i≤15 | D. | b=c,i≤15 |
2.男女生共8人,从中任选3人,出现2个男生,1个女生的概率为$\frac{15}{28}$,则其中女生人数是( )
| A. | 2人 | B. | 3人 | C. | 2人或3人 | D. | 4人 |
20.某市拟招商引资兴建一化工园区,新闻媒体对此进行了问卷调查,在所有参与调查的市民中,持“支持”、“保留”和“不支持”态度的人数如表所示:
(Ⅰ)在所有参与调查的人中,用分层抽样的方法抽取部分市民做进一步调研(不同态度的群体中亦按年龄分层抽样),已知从“保留”态度的人中抽取了19人,则在“支持”态度的群体中,年龄在30岁以上的人有多少人被抽取;
(Ⅱ)在持“不支持”态度的人中,用分层抽样的方法抽取6人做进一步的调研,将此6人看作一个总体,在这6人中任意选取2人,求至少有1人在30岁以上的概率.
| 支持 | 保留 | 不支持 | |
| 30岁以下 | 900 | 120 | 280 |
| 30岁以上(含30岁) | 300 | 260 | 140 |
(Ⅱ)在持“不支持”态度的人中,用分层抽样的方法抽取6人做进一步的调研,将此6人看作一个总体,在这6人中任意选取2人,求至少有1人在30岁以上的概率.
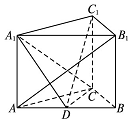 如图,在直三棱柱ABC-A1B1C1中,AB=4,AC=BC=3D为AB的中点,AB1⊥A1C
如图,在直三棱柱ABC-A1B1C1中,AB=4,AC=BC=3D为AB的中点,AB1⊥A1C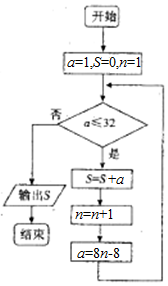 我国古代数学著作《孙子算经》中有如下的问题:“今有方物一束,外周有三十二枚,问积几何?”设每层外周枚数为a,如图是解决该问题的程序框图,则输出的结果为( )
我国古代数学著作《孙子算经》中有如下的问题:“今有方物一束,外周有三十二枚,问积几何?”设每层外周枚数为a,如图是解决该问题的程序框图,则输出的结果为( )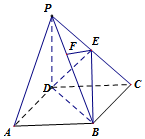 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.