题目内容
观察以下不等式：1＞
；1+
+
＞1；1+
+
…+
＞
；1+
+
+…+
＞2；1+
+
+…+
＞
；由此推测第n个不等式为（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 7 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 15 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 31 |
| 5 |
| 2 |
A、1+
| ||||||||
B、1+
| ||||||||
C、1+
| ||||||||
D、1+
|
考点：归纳推理
专题：计算题,推理和证明
分析：注意左侧的分母，右侧的分子即可．
解答：
解：∵1＞
；
1+
+
＞1；
1+
+
…+
＞
；
1+
+
+…+
＞2；
1+
+
+…+
＞
；
不等式左侧分子都为1，分母为1，2，3，4，…，2n-1；
不等式右侧分母为2，分子为n；
∴1+
+
+…+
＞
；
故选D．
| 1 |
| 2 |
1+
| 1 |
| 2 |
| 1 |
| 3 |
1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 7 |
| 3 |
| 2 |
1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 15 |
1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 31 |
| 5 |
| 2 |
不等式左侧分子都为1，分母为1，2，3，4，…，2n-1；
不等式右侧分母为2，分子为n；
∴1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n-1 |
| n |
| 2 |
故选D．
点评：本题考查了归纳推理的应用，属于基础题．
练习册系列答案
相关题目
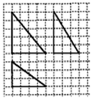如图，格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体最长的棱的长度等于（ ）A、
| ||
B、
| ||
C、5
| ||
D、2
|
关于x的不等式sin2x+acosx-a2≤1+cosx对一切x∈R恒成立，则实数a的取值范围为（ ）
A、（-1，
| ||
B、[-1，
| ||
C、（-∞，-1]∪[
| ||
D、（-∞，-1）∪（
|
在如图的各图中，每个图的两个变量具有线性相关关系的图是（ ）
| A、①② | B、①③ | C、②④ | D、②③ |
函数f（x）=
，若f（2）+f（α）=e+1，则α的所有可能值为（ ）
|
| A、1 | ||||
B、-
| ||||
C、1或-
| ||||
D、1或
|
函数f（x）=2x-
的零点在区间（ ）
| 1 |
| x |
| A、（-1，0） |
| B、（0，1） |
| C、（1，2） |
| D、（2，3） |